LeetCode Link: 101. Symmetric Tree
Problem Statement
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
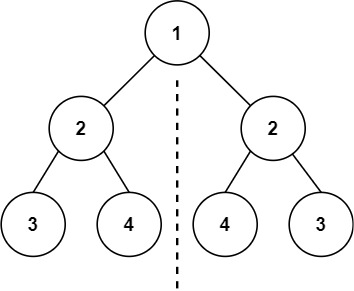
Input: root = [1,2,2,3,4,4,3]
Output: true
Example 2:
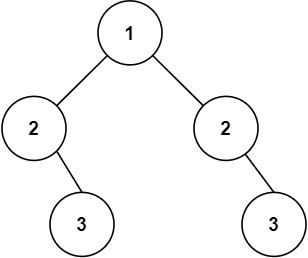
Input: root = [1,2,2,null,3,null,3]
Output: false
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. -100 <= Node.val <= 100
Introduction
When determining whether a binary tree is symmetric, it is essential to compare two subtrees: the left subtree and the right subtree of the root. The primary idea is that these two subtrees should be mirror images of each other. Instead of comparing the left and right children in isolation, we compare corresponding nodes across the subtrees (i.e., the outer and inner pairs).
Understanding this concept allows us to approach the problem by either recursively or iteratively traversing the tree and comparing the appropriate nodes.
Recursive Approach
The recursive method can be broken down into three steps:
1. Define the Recursive Function
We need a function that compares two nodes (or subtrees). In Python, we define this function to take two parameters: left and right, which correspond to nodes from the left and right subtrees of the root.
def compare(left, right):
# Base cases will be defined here2. Base Cases
Before comparing node values, we need to handle cases where one or both nodes are None:
- If both nodes are
None, the trees are symmetric at this level. - If one node is
Noneand the other is not, the tree is not symmetric. - If both nodes exist but their values differ, the tree is not symmetric.
def compare(left, right):
if left is None and right is None:
return True
if left is None or right is None:
return False
if left.val != right.val:
return False3. Recursive Comparison
After handling the base cases, we compare the outer and inner pairs:
- Outer comparison: Compare
left.leftwithright.right. - Inner comparison: Compare
left.rightwithright.left.
If both comparisons return True, then the current pair of subtrees is symmetric.
def compare(left, right):
if left is None and right is None:
return True
if left is None or right is None:
return False
if left.val != right.val:
return False
outside = compare(left.left, right.right) # Compare the outer nodes
inside = compare(left.right, right.left) # Compare the inner nodes
return outside and insideComplete Recursive Python Code
Below is the complete Python implementation using recursion:
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right) -> bool:
if left is None and right is None:
return True
if left is None or right is None:
return False
if left.val != right.val:
return False
# Compare the outer and inner pairs of nodes
outside = self.compare(left.left, right.right)
inside = self.compare(left.right, right.left)
return outside and insideNote: This recursive solution clearly lays out each logical step rather than hiding the complexities within a concise code snippet. Understanding each step is crucial when learning how to solve problems like these.
Iterative Approach
While the recursive approach is intuitive, it is also valuable to see how the problem can be solved iteratively. The iterative method uses data structures (a queue or a stack) to store pairs of nodes for comparison.
Using a Queue
The idea is to use a queue to store nodes in pairs. In each iteration, we compare the pair:
- If both nodes are
None, continue. - If one is
Noneor their values differ, returnFalse. - Otherwise, enqueue the children in the order that respects the mirror structure: first the outer pair, then the inner pair.
import collections
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque()
queue.append(root.left)
queue.append(root.right)
while queue:
leftNode = queue.popleft()
rightNode = queue.popleft()
if leftNode is None and rightNode is None:
continue
if leftNode is None or rightNode is None or leftNode.val != rightNode.val:
return False
# Enqueue the children in the correct order for comparison
queue.append(leftNode.left)
queue.append(rightNode.right)
queue.append(leftNode.right)
queue.append(rightNode.left)
return TrueUsing a Stack
The logic is similar to the queue-based approach. Instead of a queue, we use a stack to store pairs of nodes. The order of processing is reversed, but the comparison logic remains the same.
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
stack = []
stack.append(root.left)
stack.append(root.right)
while stack:
rightNode = stack.pop()
leftNode = stack.pop()
if leftNode is None and rightNode is None:
continue
if leftNode is None or rightNode is None or leftNode.val != rightNode.val:
return False
stack.append(leftNode.left)
stack.append(rightNode.right)
stack.append(leftNode.right)
stack.append(rightNode.left)
return TrueLevel-Order Traversal Approach
Another method involves performing a level-order traversal while checking if the node values at each level form a symmetric list.
import collections
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque([root.left, root.right])
while queue:
level_size = len(queue)
# The number of nodes at each level should be even for symmetry
if level_size % 2 != 0:
return False
level_vals = []
for _ in range(level_size):
node = queue.popleft()
if node:
level_vals.append(node.val)
queue.append(node.left)
queue.append(node.right)
else:
level_vals.append(None)
# Check if the level values are symmetric
if level_vals != level_vals[::-1]:
return False
return TrueConclusion
In this post, we delved into the problem of determining whether a binary tree is symmetric. We explored two main approaches:
- Recursive Approach: Emphasizes the importance of comparing both the outer and inner nodes recursively.
- Iterative Approach: Demonstrates the use of queues and stacks to iteratively compare node pairs.
Each method not only provides a solution but also highlights the underlying logic necessary to understand and solve similar binary tree problems. When practicing, it is essential to think through each step rather than simply copying code.
Related Problems
If you enjoyed this discussion, you might also be interested in the following problems:
By exploring these related challenges, you can further deepen your understanding of binary tree operations and recursive thinking in Python.
Happy LeetCoding!

Discussion