Summary of Arrays

Basics of Array

Arrays are a very fundamental data structure. In interviews, questions about arrays generally aren't difficult in terms of logic; they mainly test your ability to handle code.

In other words, the idea is simple, but implementing it might not be as straightforward.

First, you need to understand how arrays are stored in memory to truly grasp array-related interview questions.

An array is a collection of data of the same type stored in contiguous memory space.

Arrays allow easy access to elements through index-based referencing.

Here's an example of a character array, as shown:

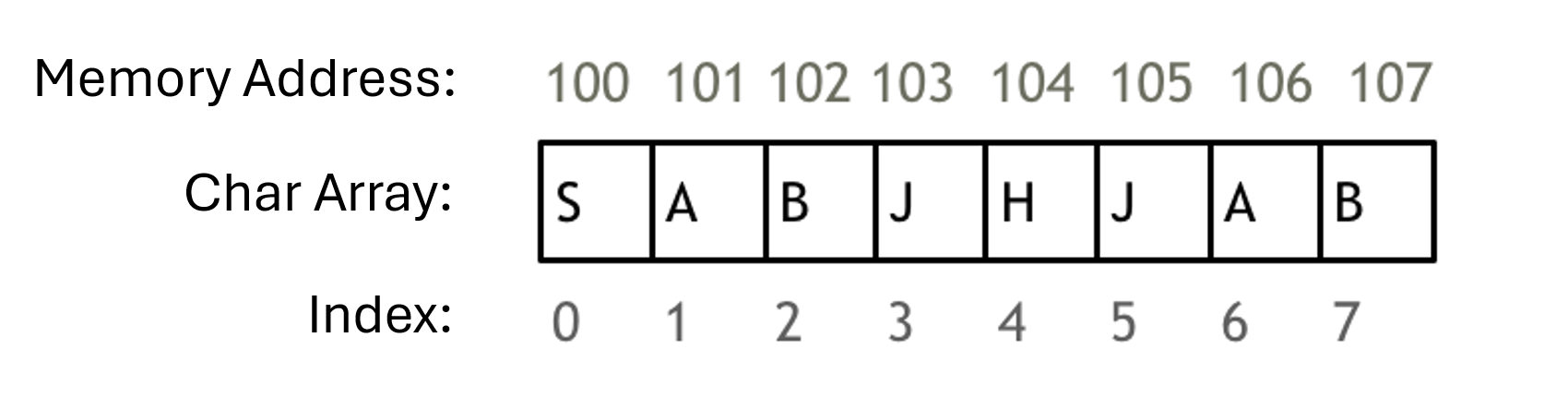
Two points to note are:

Array indices start from 0.
The memory addresses of arrays are contiguous.

It is precisely because the memory addresses of arrays are contiguous that when we delete or add elements, we inevitably have to move the addresses of other elements.

For example, to delete the element at index 3, all elements after index 3 need to be moved, as shown in the diagram:

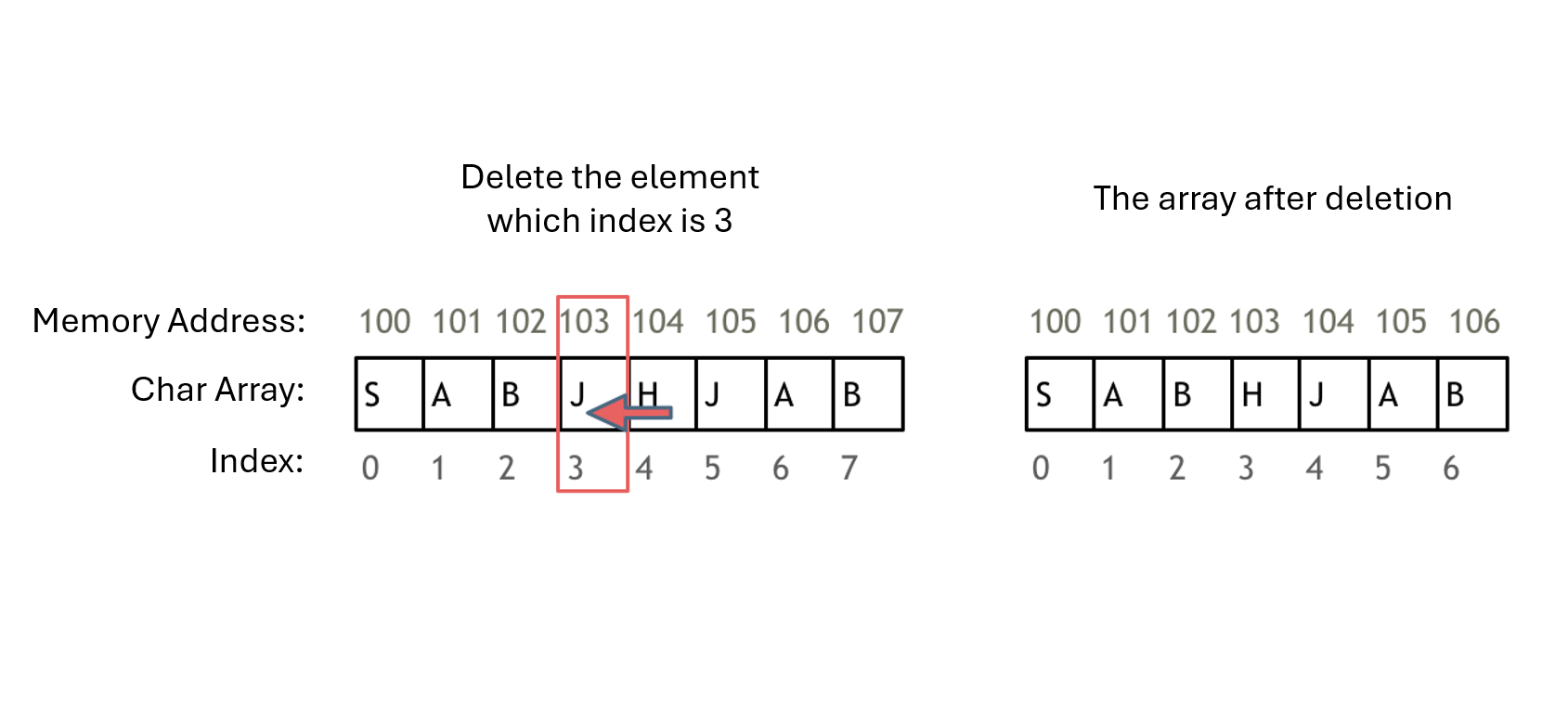
The elements of the array cannot be deleted, they can only be overwritten.

Now, let's dive into a 2D array. The image below illustrates how elements are organized:

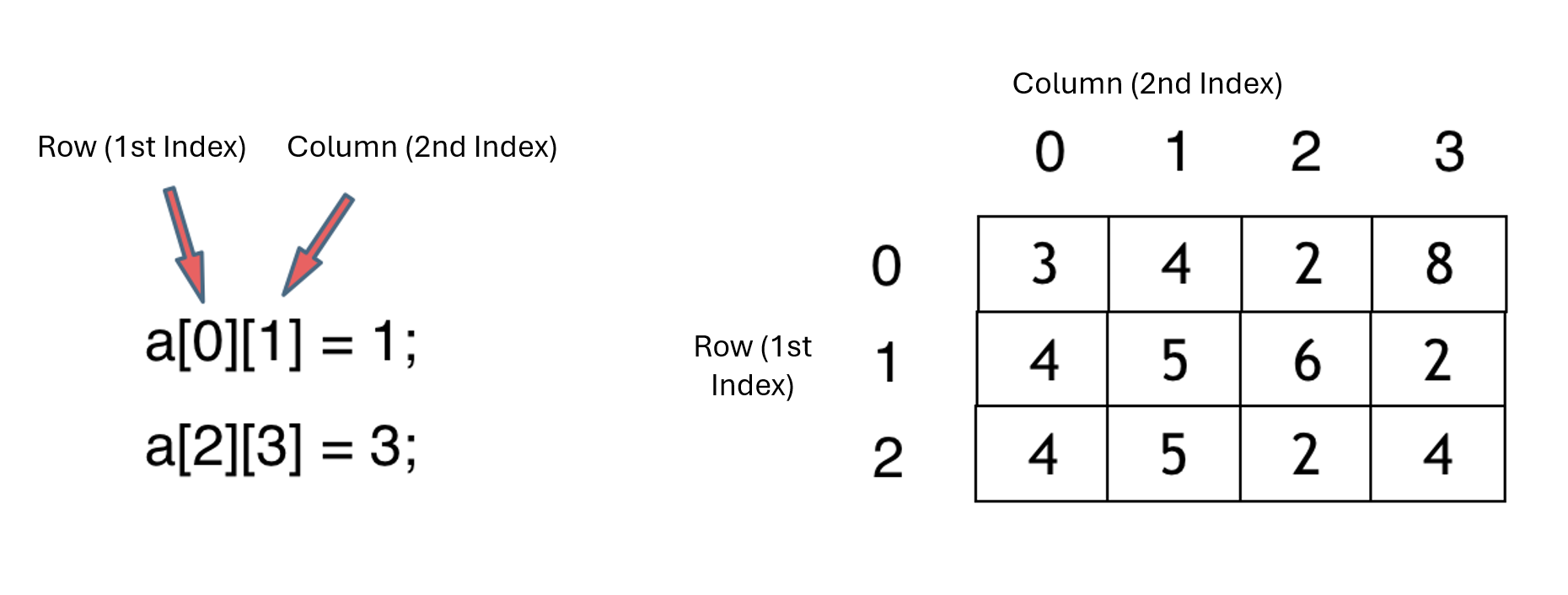
Are 2D Arrays in Memory Contiguous?

In Python, a list of lists (2D array) is stored as follows:

The outer list contains references/pointers to the inner lists
Each inner list is a separate list object stored in memory
The inner lists can be stored in non-contiguous memory locations

However, within each inner list, the elements themselves are stored contiguously in memory (assuming they are of compatible types like numbers).

Here's a visualization to help explain:

matrix = [
    [1, 2, 3],  # Inner list 1 - contiguous in memory
    [4, 5, 6],  # Inner list 2 - contiguous in memory
    [7, 8, 9]   # Inner list 3 - contiguous in memory
]

The outer list contains pointers to these three inner lists, and while the inner lists themselves might not be adjacent in memory, the elements within each inner list (1,2,3), (4,5,6), and (7,8,9) are stored contiguously.

This is different from languages like C or Fortran, where a 2D array is guaranteed to be one continuous block of memory. If you need that behavior in Python, you would typically use NumPy arrays (numpy.ndarray), which do provide contiguous memory storage for multi-dimensional arrays.

Classic Array Problems

In interviews, arrays are a fundamental data structure that is essential to test.

In fact, the problems related to arrays are generally simple in concept, but achieving efficiency is not easy.

We have previously explained four classic array problems, each representing a type and a way of thinking.

Binary Search

Every time I encounter binary search, it's easy to understand but hard to write

This problem is mainly about basic array operations. The idea is simple, but the pass rate isn't high for an easy question, so don't underestimate it.

You can use a brute force solution to solve this problem. If you're aiming for a more optimal algorithm, try using binary search.

Brute force time complexity: O(n)
Binary search time complexity: O(logn)

In this problem, we discussed the loop invariant principle; only by adhering to the definition of intervals in loops can you clearly grasp various details within them.

Binary search is a common topic in algorithm interviews. It's recommended to practice your ability to manually implement binary searches through this problem.

Note: Pay attention to boundary conditions

Left Closed, Right Closed Interval

right = nums.size() - 1
while (left <= right):
    middle = (left + right) / 2
    if nums[middle] == target:
        return middle
    elif nums[middle] < target:
        left = middle + 1
    else:
        right = middle - 1

Left Closed, Right Open Interval

right = nums.size()
while (left < right):
    middle = (left + right) / 2
    if nums[middle] == target:
        return middle
    elif nums[middle] < target:
        left = middle + 1
    else:
        right = middle

Two-pointer

Two-pointer method (fast and slow pointers): Completes the work of two for-loops with one fast pointer and one slow pointer under a single for-loop.

Brute force time complexity: O(n^2)
Two-pointer time complexity: O(n)

The confusion surrounding the inability to delete elements from arrays stems from the fact that arrays occupy a continuous block of memory addresses and do not allow for the release of individual elements. Instead, the entire array must be released, with the memory stack space typically being reclaimed upon the program's termination.

The two-pointer method (fast and slow pointers) is very common in operations on arrays and linked lists; many interview questions testing these operations use this method.

Sliding Window

This question introduces another important concept in array manipulation: sliding window.

Brute force time complexity: O(n^2)
Sliding window time complexity: O(n)

In this question, it's essential to understand how the sliding window moves its starting position dynamically updating its size until finding the smallest length meeting conditions.

The brilliance of the sliding window lies in its ability to continuously adjust the starting position of the subsequence based on the current subsequence and size, thereby reducing the brute force solution from O(n^2) to O(n).

If you've never encountered such methods before thinking up similar approaches might seem challenging yet ingenious nonetheless!

Simulation Behavior

Simulation problems frequently occur with arrays and often do not involve complex algorithms, but rather pure simulation, which thoroughly tests one's coding skills. This brings us back to the familiar concept of the "Loop Invariant Principle," which once again proves to be crucial in various programming endeavors.

Many may find themselves amidst situations where it feels like the problem has a lot of boundary adjustments, with wave after wave of judgments, finding boundaries, and patching things up. After finally getting it to run through, the code is extremely redundant and lacks structure. In fact, the real solution to the problem should be concise or principled. You can experience this point in this question.

Prefix Sum

Prefix sums provide straightforward and practical insights, although those unfamiliar with them may initially find it challenging to envision multi-dimensional solutions. This broadens perspectives while keeping the difficulty level manageable, making them excellent exercises overall.