Reverse Linked List
Master three different approaches to solving LeetCode's Reverse Linked List problem (#206). Learn the efficient two-pointer technique, recursive method, and stack-based solution with detailed explanations and Python implementations. Perfect for coding interviews and data structure practice.
LeetCode Link: 206. Reverse Linked List
Problem Definition
Given the head of a singly linked list, reverse the list, and return the reversed list.
Example 1:
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]
Example 2:
Input: head = [1,2]
Output: [2,1]
Example 3:
Input: head = []
Output: []
Constraints:
- The number of nodes in the list is the range
[0, 5000]. -5000 <= Node.val <= 5000
Thought Process
If a new linked list is defined to reverse the elements of the list, it actually wastes memory space.
In fact, you only need to change the direction of the next pointer in the linked list to directly reverse it without redefining a new linked list, as shown in the figure:
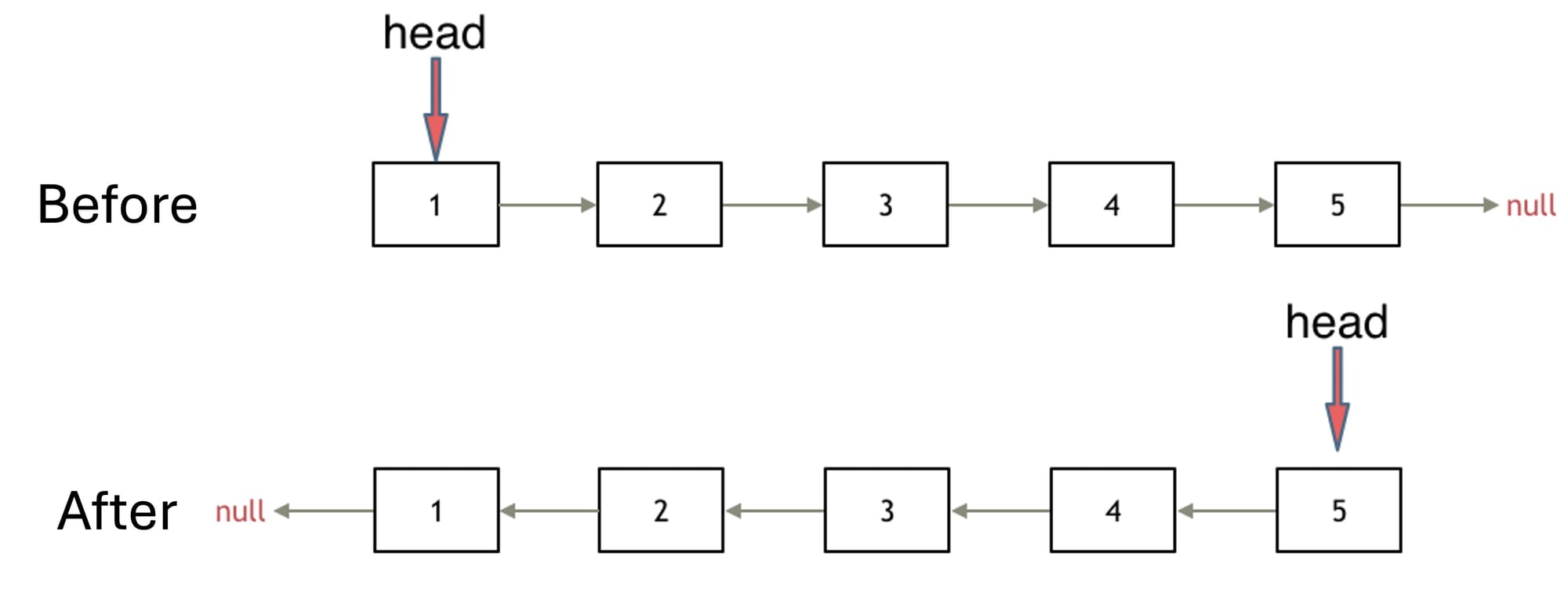
First, we define a pointer cur to point to the head node, and then we define another pointer pre, initialized to null.
Now we begin the reversal. First, we save cur->next in a temporary pointer tmp to hold this node.
Why do we need to save this node? Because we are about to change the direction of cur->next. We set cur->next to point to pre, which completes the reversal of the first node.
Next, we continue with the following code logic in a loop, moving pre and cur pointers forward.
Finally, when cur points to null, the loop ends, and the list is fully reversed. At this point, we return the pre pointer, which now points to the new head node of the reversed list.
Solution 1 - Double Pointer
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
cur = head
pre = None
while cur:
temp = cur.next # Save the next node of cur, as we are about to change cur->next
cur.next = pre # Reverse the pointer
# Update pre and cur pointers
pre = cur
cur = temp
return preTime Complexity: O(n)
Space Complexity: O(1)
Solution 2 - Recursive
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
return self.reverse(head, None)
def reverse(self, cur: ListNode, pre: ListNode) -> ListNode:
if cur == None:
return pre
temp = cur.next
cur.next = pre
return self.reverse(temp, cur)The recursive approach is relatively abstract, but it follows the same logic as the two-pointer method. The process involves continually pointing cur to pre and ends when cur is null.
The key lies in the initialization, which can sometimes be hard to understand. In the two-pointer method, we initialize with cur = head and pre = null. In the recursive method, the initialization logic is the same; only the writing style changes.
Solution 3 - Stack
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def reverseList(self, head: ListNode) -> ListNode:
# If the list is empty, return None
if head is None:
return None
# If there is only one element, return it directly
if head.next is None:
return head
# Create a stack and push all nodes onto the stack
stack = []
cur = head
while cur:
stack.append(cur)
cur = cur.next
# Create a dummy head
p_head = ListNode(0)
cur = p_head
# Pop nodes from the stack to reverse the list
while stack:
node = stack.pop()
cur.next = node
cur = cur.next
# Set the next of the last node to None
cur.next = None
return p_head.nextHow It Works:
- This solution pushes each node onto a stack and then pops each node from the stack to reverse the order of the nodes.
- After all nodes are popped from the stack, the
nextpointer of the last node is set toNoneto mark the end of the reversed list.
Pros:
- Simplicity: The logic is simple and straightforward, using the stack to reverse the node order.
Cons:
- Space Complexity: This solution has a space complexity of O(n) due to the stack, which stores all nodes of the list.
- Not Optimal for Space: Since we’re using additional memory (the stack), this approach is not as space-efficient as an in-place reversal (e.g., using the two-pointer or recursive method).
Conclusion: This solution works but is not optimal because it requires extra space proportional to the number of nodes. An in-place reversal solution with O(1) space complexity would be preferable for efficiency, especially for large lists. However, if simplicity and readability are the priority, this stack-based approach is an acceptable alternative.
Discussion