Minimum Size Subarray Sum
Solve LeetCode 209: Minimum Size Subarray Sum efficiently using the sliding window technique. This approach reduces time complexity to O(n) by dynamically adjusting the window’s size to find the smallest subarray with a sum ≥ target. Ideal for arrays with positive integers.
Problem Definition
LeetCode Link: 209. Minimum Size Subarray Sum
Given an array of positive integers nums and a positive integer target, return the minimal length of a
subarray whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.
Example 1:
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.
Example 2:
Input: target = 4, nums = [1,4,4]
Output: 1
Example 3:
Input: target = 11, nums = [1,1,1,1,1,1,1,1]
Output: 0
Constraints:
1 <= target <= 1091 <= nums.length <= 1051 <= nums[i] <= 104
Thought Process
Brute Force
The brute force solution to this problem is of course two for loops, continuously searching for subsequences that meet the conditions, and the time complexity is obviously O(n^2).
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
l = len(nums)
min_len = float('inf')
for i in range(l):
cur_sum = 0
for j in range(i, l):
cur_sum += nums[j]
if cur_sum >= s:
min_len = min(min_len, j - i + 1)
break
return min_len if min_len != float('inf') else 0Now this method won't be passed on LeetCode as it will trigger a timeout error.
Sliding Window
Next, we will introduce another important method in array operations: sliding window.
The so-called sliding window is the continuous adjustment of the starting and ending positions of a subsequence to derive the desired result.
In the brute force solution, one for loop slides the starting position of the window, while another for loop defines its ending position, using two for loops to complete a process of continuously searching through intervals.
So how can we accomplish this operation with just one for loop?
First, we need to consider whether this single for loop should represent the starting or ending position of the sliding window.
If we only use one for loop to represent the starting position of the sliding window, how do we traverse through all possible ending positions?
At this point, it’s inevitable that we'll fall back into the cycle of brute force solutions again.
Therefore, if we're using just one for loop, then its index must represent the ending position of the sliding window.
Now comes the question: how does the starting position of the sliding window move?
Here we'll take an example from our problem: let s=7 and our array be [2, 3, 1, 2, 4, 3]. Let's look at how to find it step by step:
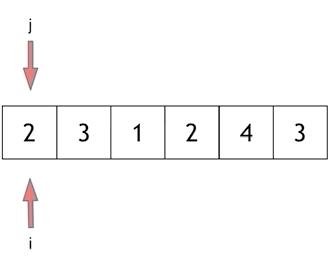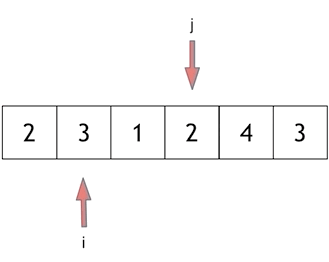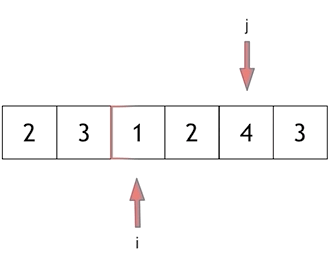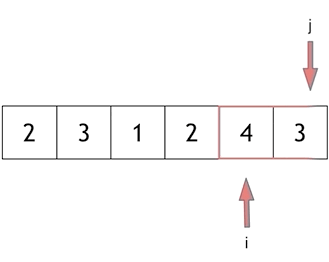
Finally, 4 and 3 are the shortest distances.
In fact, from the animation, we can see that the sliding window can also be understood as a type of two-pointer method! However, this solution is more like moving a window, so it is more appropriate to call it a sliding window.
In this problem, implementing the sliding window mainly involves determining the following three points:
- What is inside the window?
- How to move the starting position of the window?
- How to move the ending position of the window?
The window is defined as the smallest continuous subarray whose sum ≥ s.
How to move the starting position of the window: If the current value in the window is greater than or equal to s, then we need to move forward (which means it should be shrunk).
How to move the ending position of the window: The ending position of the window corresponds to a pointer traversing through an array, which refers to an index in a for loop.
The key to solving this problem lies in how to move the starting position ofthewindow, as shown inthe diagram:
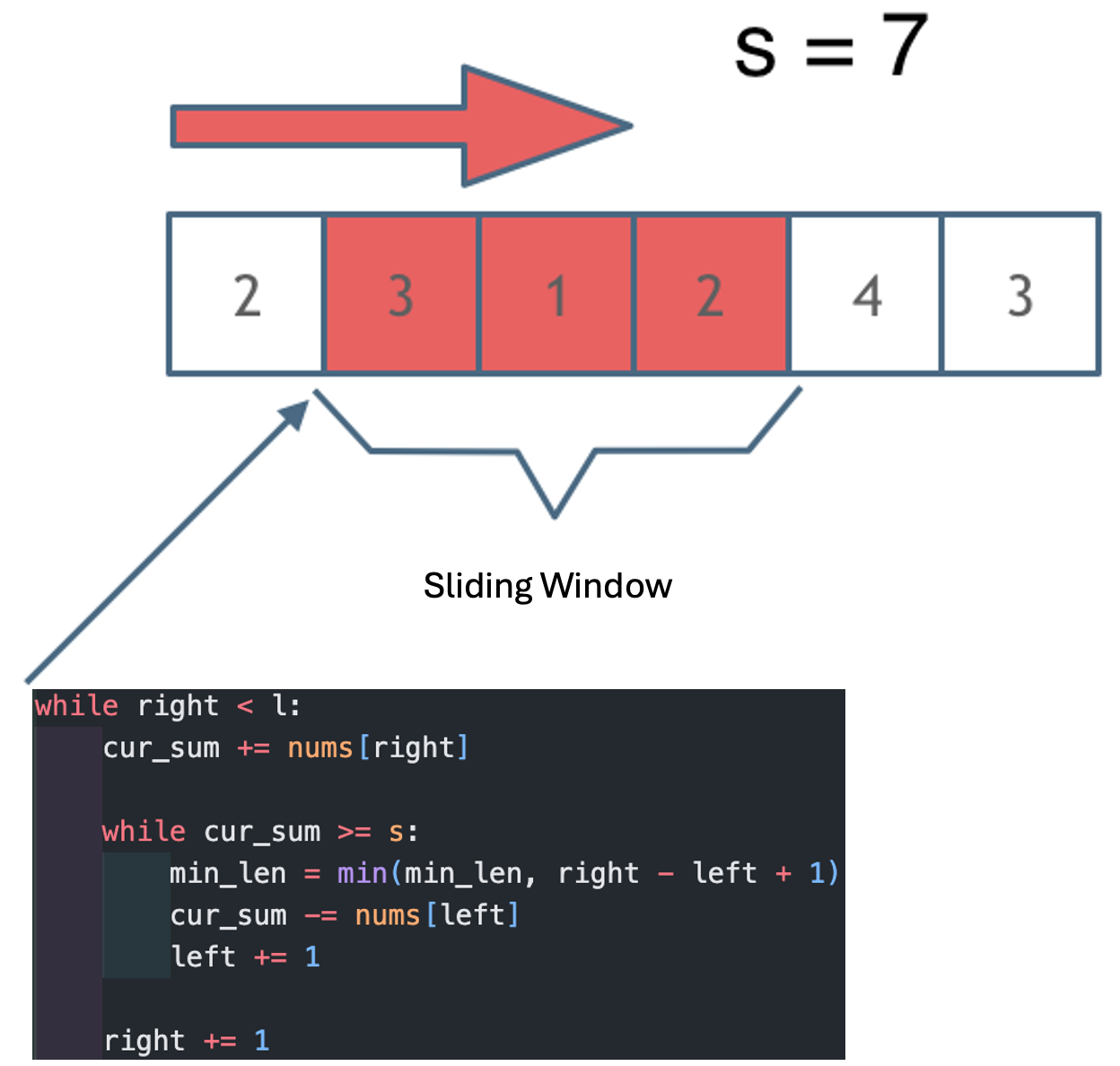
The brilliance of the sliding window technique lies in continuously adjusting the starting position of the subsequence based on the current subsequence and its size, thereby reducing the O(n^2) brute force solution to O(n).
The code is as follows:
class Solution:
def minSubArrayLen(self, s: int, nums: List[int]) -> int:
l = len(nums)
left = 0
right = 0
min_len = float('inf')
cur_sum = 0
while right < l:
cur_sum += nums[right]
while cur_sum >= s:
min_len = min(min_len, right - left + 1)
cur_sum -= nums[left]
left += 1
right += 1
return min_len if min_len != float('inf') else 0- Time complexity: O(n)
- Space complexity: O(1)
Some people may wonder why the time complexity is O(n).
Don't think that putting a while loop inside a for loop means it's O(n^2); it mainly depends on how many times each element is operated on. Each element enters and exits the sliding window once, so each element is operated on twice, which makes the time complexity 2 × n, or O(n).
Discussion