LeetCode Link: 104. Maximum Depth of Binary Tree
Problem Statement
Given the root of a binary tree, return its maximum depth.
A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:
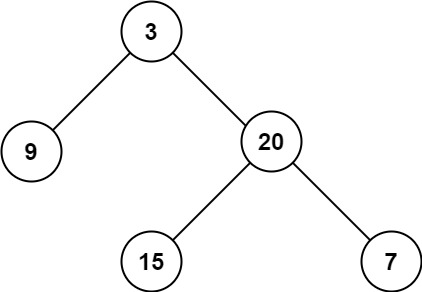
Input: root = [3,9,20,null,null,15,7]
Output: 3
Example 2:
Input: root = [1,null,2]
Output: 2
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. -100 <= Node.val <= 100
Understanding the Problem
Before diving into the solution, let's clarify two important concepts:
- Depth: The distance from the root to a given node
- Height: The distance from a given node to the deepest leaf
Interestingly, the maximum depth of a binary tree is the same as the height of the root node. This means we can approach this problem from two different angles:
Solution Approaches
1. Recursive Approach (DFS)
There are two ways to implement the recursive approach:
Approach 1: Bottom-up (Post-order Traversal)
This is the most intuitive approach. We calculate the height of the tree by:
- Recursively finding the height of the left subtree
- Recursively finding the height of the right subtree
- Taking the maximum of these two heights and adding 1 (for the current node)
class Solution:
def maxDepth(self, root: TreeNode) -> int:
# Base case: If the node is None, height is 0
if not root:
return 0
# Recursively calculate the height of left and right subtrees
left_height = self.maxDepth(root.left) # Left
right_height = self.maxDepth(root.right) # Right
# Return the maximum height + 1 (for the current node)
return 1 + max(left_height, right_height) # MiddleThis solution uses the post-order traversal (left → right → middle) pattern, which is particularly well-suited for solving tree height problems.
Approach 2: Top-down (Pre-order Traversal)
We can also solve this using a pre-order traversal approach:
class Solution:
def maxDepth(self, root: TreeNode) -> int:
# Initialize result
self.result = 0
def getDepth(node, depth):
if not node:
return
# Update result if current depth is greater
self.result = max(self.result, depth) # Middle
# Recursively check left and right subtrees
getDepth(node.left, depth + 1) # Left
getDepth(node.right, depth + 1) # Right
if not root:
return 0
getDepth(root, 1)
return self.resultThis approach clearly shows the backtracking process when calculating depth. We pass the current depth to each recursive call and update our global result variable when we find a deeper path.
2. Iterative Approach (BFS - Level Order Traversal)
Since the maximum depth equals the number of levels in the tree, we can use level-order traversal:
from collections import deque
class Solution:
def maxDepth(self, root: TreeNode) -> int:
if not root:
return 0
depth = 0
queue = deque([root])
while queue:
# Process all nodes at the current level
size = len(queue)
depth += 1 # Increment depth for each level
for _ in range(size):
node = queue.popleft()
# Add children to the queue
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return depthThis approach is very intuitive: we simply count the number of levels we process during the traversal.
Time and Space Complexity Analysis
Recursive Approaches:
- Time Complexity: O(n) where n is the number of nodes in the tree
- Space Complexity: O(h) where h is the height of the tree (due to the recursion stack)
- In the worst case of a skewed tree, this becomes O(n)
- In the best case of a balanced tree, this becomes O(log n)
Iterative Approach:
- Time Complexity: O(n) where n is the number of nodes in the tree
- Space Complexity: O(w) where w is the maximum width of the tree
- In the worst case, this could be O(n/2) ≈ O(n) for a complete binary tree
- In the best case, this becomes O(1) for a skewed tree

Discussion