Problem Definition
Given the head nodes of two singly linked lists, headA and headB, please find and return the starting node where the two singly linked lists intersect. If there is no intersection point, return null.
The diagram shows that the two linked lists begin to intersect at node c1:
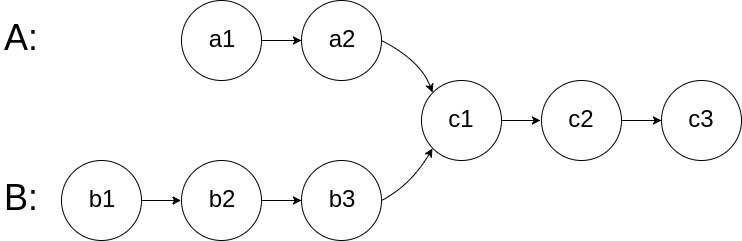
The data ensures that there are no cycles in the entire chain structure.
Note that after the function returns a result, the linked list must maintain its original structure.
Example 1:
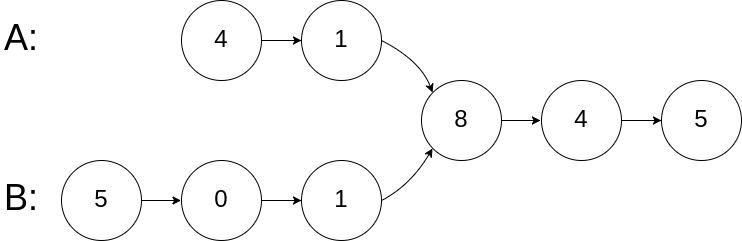
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Intersected at '8'
Explanation: The value of the intersection node is 8 (note that if two linked lists intersect it cannot be 0).
Starting from their respective heads, linked list A is [4,1,8,4,5] and linked list B is [5,0,1,8,4 ,5].
In A there are 2 nodes before the intersection node; in B there are 3 nodes before the intersection node.
Example 2:
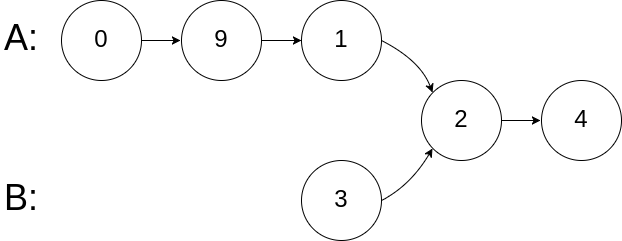
Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Intersected at '2'
Explanation: The value of the intersection node is 2 (note that if two linked lists intersect it cannot be 0). Starting from their respective heads, linked list A is [0,9,1,2,4] and linked list B is [3,2,4]. In A there are 3 nodes before the intersection node; in B there is 1 node before the intersection node.
Example 3:
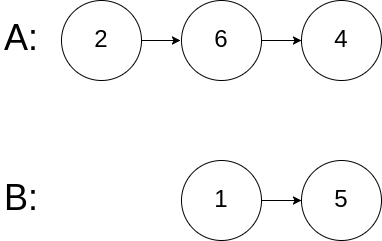
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Explanation: Starting from the head of each list, linked list A is [2,6,4] and linked list B is [1,5]. Since these two linked lists do not intersect, intersectVal must be 0 and skipA and skipB can be any values. These two linked lists do not intersect; therefore, return null.
Thought Process
If the two linked lists are not of equal length
If they intersect:
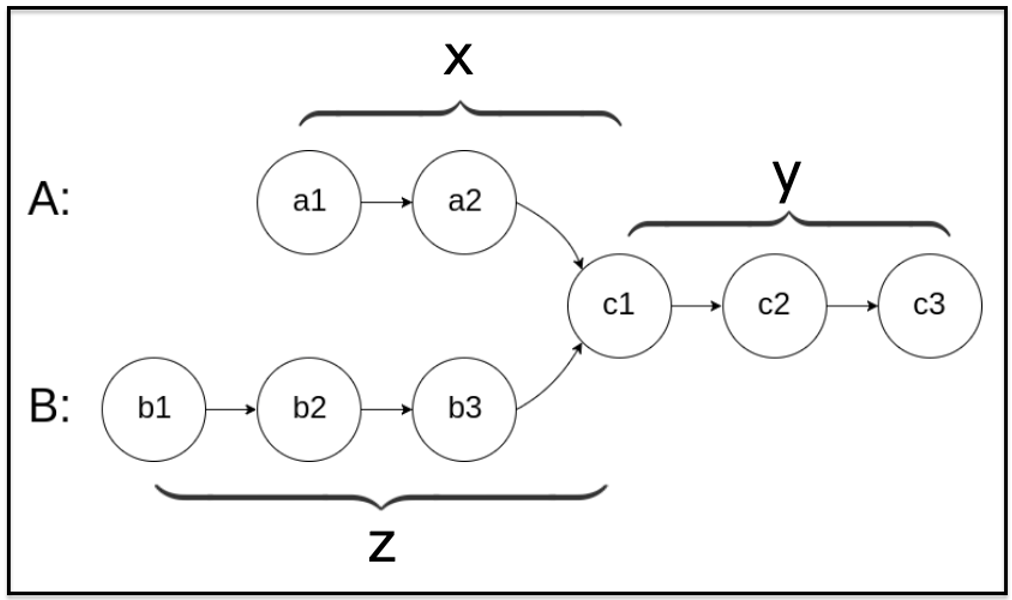
As shown in the above diagram, x, y, z represent the number of steps corresponding to each segment.
Use pointer 1 to traverse A and then traverse B. The route is ⟨a1, a2, c1, c2, c3, Nill, b1, b2, b3, c1⟩.
At the same time use pointer 2 to traverse B and then traverse A. The route is ⟨b1,b2,b3,c1,c2,c3,Null,a1,a2,c1⟩.
It can be concluded that:
- Pointer 1 reaches intersection point c₁ after moving
x+y+2+zsteps. The+2corresponds to the transfer process⟨c₃,Null,b₁⟩. - Similarly, pointer 2 reaches intersection point c₁ after moving
z+y+2+xsteps,
allowing both pointers to meet.
Time complexity: Θ(x+y+z+2)=Θ(x+y+z+y)=Θ(m+n)
If they do not intersect

The movement rules for pointers 1 and 2 are the same as above. The specific path of pointer 1 is a₁ ⇝ a₅ → Null → b₁ ⇝ b₆ → Null.
⇝ Indicates that there are several nodes in between, which are omitted for simplicity.
Meanwhile, the path of pointer 2 is b1 ⇝ b6 → Null → a1 ⇝ a5 → Nil.
That is, after m+n+1 steps, both pointers 1 and 2 point to Null, indirectly achieving pointer intersection.
Time complexity: Θ(m+n)
If the two linked lists are of equal length
Continue to advance the two pointers from a1 and b1 at the same speed.
If they intersect

The two pointers will meet at c1.
Time complexity: O(m)
If they do not intersect

When pointer 1 traverses to the child node of a₆, which is Null, pointer 2 will also point to the child node of b₆, which is Null. Both pointing to Null indirectly achieves the meeting of pointers.
Time complexity: Θ(m)
Solution
class Solution:
def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:
nodeA = headA
nodeB = headB
while nodeA != nodeB:
if nodeA:
nodeA = nodeA.next
else:
nodeA = headB
if nodeB:
nodeB = nodeB.next
else:
nodeB = headA
return nodeA
Discussion