LeetCode Link: 142. Linked List Cycle II
Problem Definition
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:
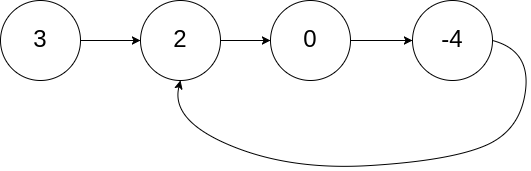
Input: head = [3,2,0,-4], pos = 1
Output: tail connects to node index 1
Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
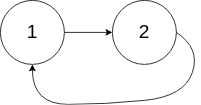
Input: head = [1,2], pos = 0
Output: tail connects to node index 0
Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1
Output: no cycle
Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked list.
Thought Process
This problem not only tests the manipulation of linked lists but also requires some mathematical operations.
The main points of examination are:
- Determining if a linked list has a cycle
- If there is a cycle, how to find the entry point of this cycle
Determine if a Linked List Has a Cycle
You can use the fast and slow pointer method by defining fast and slow pointers, starting from the head node. The fast pointer moves two nodes at a time, while the slow pointer moves one node at a time. If the fast and slow pointers meet along the way, it indicates that there is a cycle in this linked list.
Why do they definitely meet within the cycle when fast moves two nodes and slow moves one node, instead of always missing each other?
First and foremost: The fast pointer will definitely enter the cycle first. If the fast and slow pointers meet, it must be within the cycle; this is beyond doubt.
The fast and slow pointers are bound to meet. This is because fast takes two steps while slow takes one step. In fact, relative to slow, fast approaches slow node by node, so fast will definitely coincide with slow.
If there is a loop, how to find the entry point of this loop
At this point, it can already be determined whether the linked list has a loop. Next, we need to find the entry point of this loop.
Assume that the number of nodes from the head node to the circular entry node is x. The number of nodes from the circular entry node to where fast and slow pointers meet is y. The number of nodes from the meeting point back to the circular entry node is z. As shown in the figure:
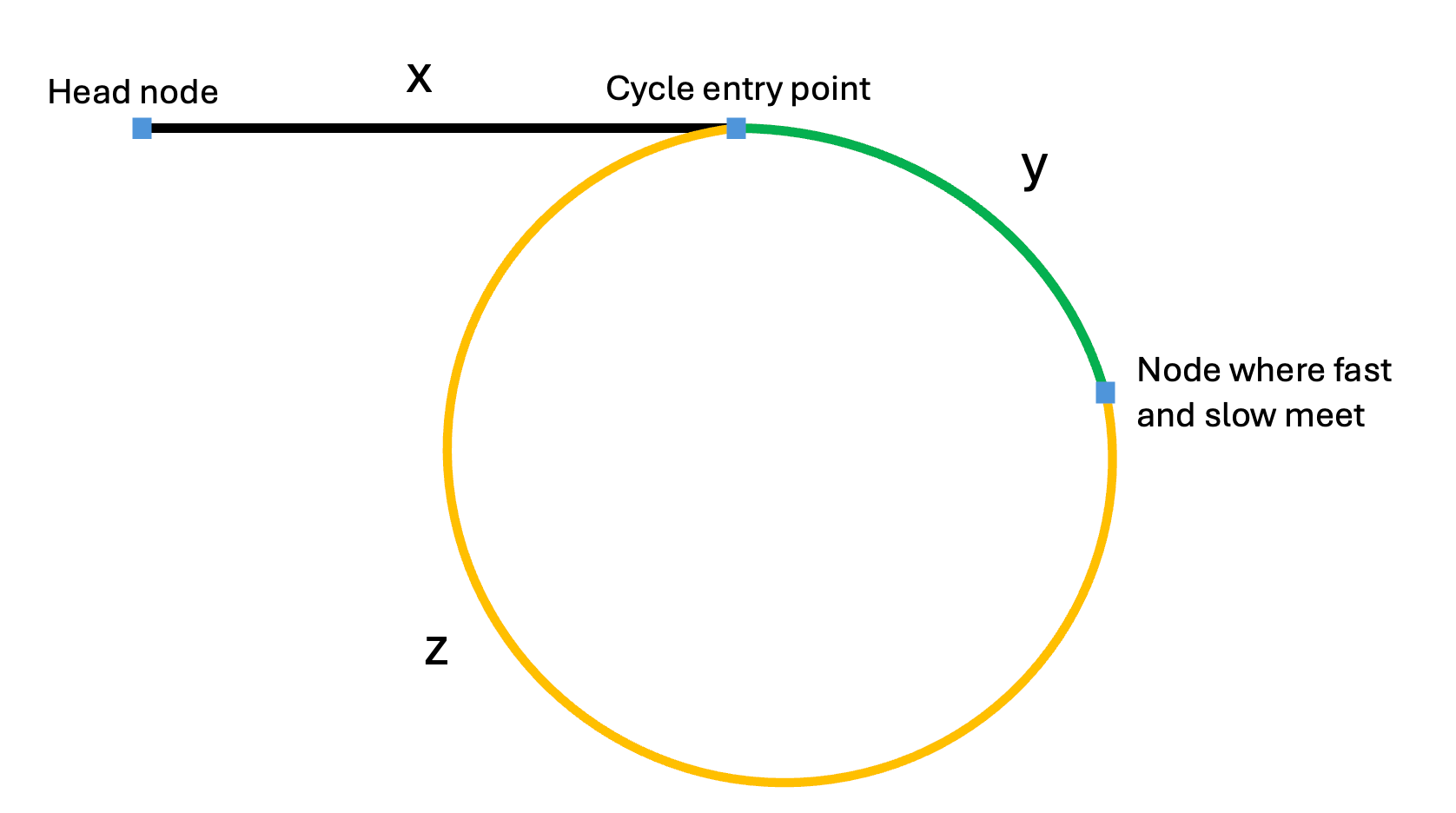
So, when they meet:
The number of nodes the slow pointer has traversed is x + y,
The number of nodes the fast pointer has traversed: x + y + n(y + z), where n is the number of laps the fast pointer made in the loop before meeting the slow pointer, and (y+z) is the number of nodes in one lap A.
Since the fast pointer moves two nodes at a time and the slow pointer moves one node at a time, we have that:
(x + y) * 2 = x + y + n(y + z)
Subtracting (x+y) from both sides gives: x + y = n(y+z)
To find the entry point to the loop, we need to solve for x because x represents the distance from head node to loop entry node.
Rearranging for x gives x = n(y+z) - y,
Factoring out (y+z) from n(y+z) results in this formula: x = (n-1)(y+z) + z. Note that here, n must be greater than or equal to 1 because it takes at least one extra lap for fast pointer to meet slow pointer.
What does this formula indicate?
Let's take an example with n=1. This means after making one full circle inside loop, fast meets slow again.
When n=1, formula simplifies to x=z.
This implies starting a new pointer from head node and another from meeting point; if both move one step each simultaneously, they will meet exactly at loop's entry.
Thus, define index1 starting at meeting point and index2 starting at head node. Move them together step by step until they meet; their meeting point will be entrance into circular part.
So, what happens if n is greater than 1? It means the fast pointer meets the slow pointer after making n loops in the cycle.
In fact, this situation is the same as when n equals 1. You can still find the entry node of the cycle using this method. The only difference is that index1 makes (n-1) additional loops in the cycle before meeting index2, and their meeting point is still the entry node of the cycle.
Solution 1 - Fast and Slow Pointer
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
# If there is a cycle, the slow and fast pointers will eventually meet
if slow == fast:
# Move one of the pointers back to the start of the list
slow = head
while slow != fast:
slow = slow.next
fast = fast.next
return slow
# If there is no cycle, return None
return NoneSolution 2 - Python set()
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def detectCycle(self, head: ListNode) -> ListNode:
visited = set()
while head:
if head in visited:
return head
visited.add(head)
head = head.next
return NoneThis solution will work because it relies on the property of Python's set data structure, which checks for object identity, not value equality, when storing and comparing objects like nodes in a linked list. Let me explain this further.
Why the Solution Works:
- Node Identity vs. Value Equality:
- In Python,
head in visitedchecks whether the specific object (i.e., the memory address of theheadnode) is already in the set. - Even if two nodes have the same value (e.g.,
val = 2), they are treated as different objects if they occupy different locations in memory. - The
setdoes not compare node values; it compares the object identity (id(head)).
- In Python,
- Cycle Detection:
- As the loop progresses, every unique node encountered is added to the
visitedset. - If the
headpointer revisits a node (because of a cycle), that node will already be in thevisitedset, and the code will return that node as the entry point of the cycle.
- As the loop progresses, every unique node encountered is added to the
- Handling Non-Cyclic Lists:
- If there is no cycle, the
headpointer will eventually becomeNone, and the loop will terminate, returningNoneto indicate no cycle.
- If there is no cycle, the
So, if there are two nodes with the same value (for example, 2) but they are not the entry point of the cycle, the solution will still work because:
- Each node is treated as a unique object based on its memory location, not its value.
- Two nodes with the same value but different memory addresses will be added to the
visitedset as separate entries.

Discussion