Problem Definition
LeetCode Link: 704. Binary Search
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Example 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
Constraints:
1 <= nums.length <= 104-104 < nums[i], target < 104- All the integers in
numsare unique. numsis sorted in ascending order.
Thought Process
The premise of this problem is that the array is a sorted array, and the problem also emphasizes that there are no duplicate elements in the array. Because once there are duplicate elements, the index returned by binary search may not be unique. These are all prerequisites for using binary search. When everyone sees that the description of the problem meets these conditions, they should consider whether binary search can be used.
Binary search involves many boundary conditions; its logic is relatively simple, but it can be difficult to implement correctly. For example, should it be while(left < right) or while(left <= right)? Should we set right = middle or right = middle - 1?
People often get confused when writing binary search mainly because they haven't clearly defined the intervals; defining intervals is an invariant. During the process of binary searching, maintaining invariants means that every time boundaries are handled during while searching, operations must adhere to interval definitions—this follows the rule of loop invariants.
When writing a binary search, interval definitions generally fall into two types: closed on both sides [left, right], or closed on one side and open on another [left, right).
Below are two different implementations of binary search based on these two types of interval definitions.
First Implementation of Binary Search
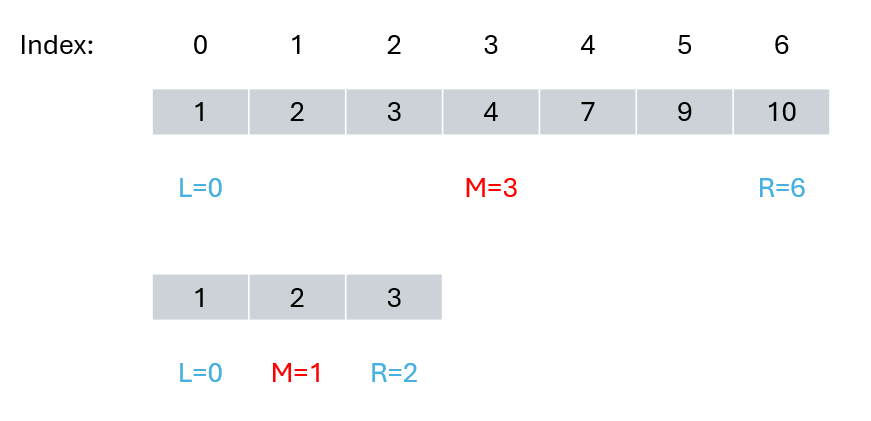
In this first implementation, we define target as being within a closed interval on both sides—specifically [left, right] (this is very important).
The definition of this interval determines how to write the code for binary search; because we define target within [left, right], there are two key points:
- Use
while (left <= right), since left == right has significance. - If
(nums[middle] > target), then assignrighttomiddle - 1, because nums[middle] is not equal to target at this point then our next left interval's end index must be middle - 1.
For example, in an array: [1,2,3,4,7,9,10] looking for element 2:
The code is as follows: (with detailed comments)
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1 # Define the target in a closed interval [left, right]
while left <= right:
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle - 1 # The target is in the left interval, so [left, middle - 1].
elif nums[middle] < target:
left = middle + 1 # The target is in the right interval, so[middle + 1, right]
else:
return middle # Find the target value in the array and return the index directly.
return -1 # Did not find the target value- Time complexity: O(log n)
- Space complexity: O(1)
Second Implementation of Binary Search
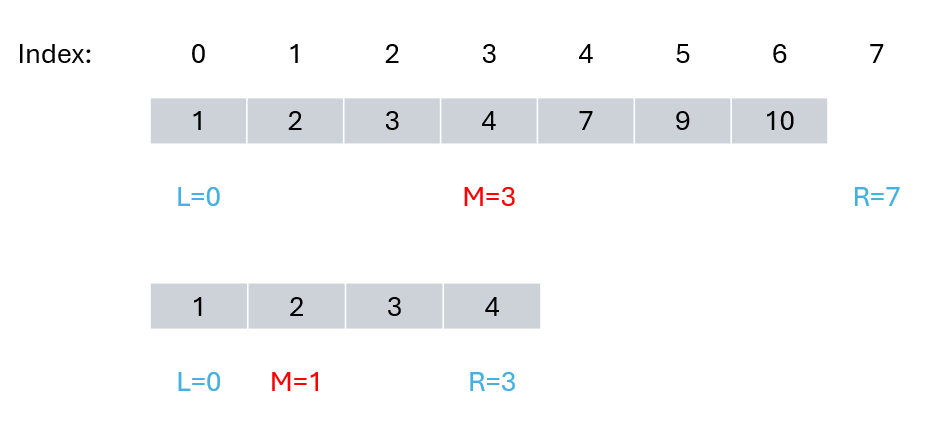
If we define the target within a closed-left, open-right interval, that is [left, right), then the boundary handling method of binary search is quite different.
There are two points:
- while (left < right), here we use < because left == right has no meaning in the interval [left, right)
- if (nums[middle] > target) update right to middle, because the current nums[middle] is not equal to target; we continue searching in the left interval. Since the searching interval is closed on the left and open on the right, we update right to middle, which means: the next query interval will not compare nums[middle].
In an array: [1,2,3,4,7,9,10] looking for element 2 as shown in the figure: (Note the difference from Method One)
The code is as follows:
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) # Define the target in a closed interval on the left and an open interval on the right, that is: [left, right)
while left < right: # Because when left == right, the space [left, right) is invalid, so < is used.
middle = left + (right - left) // 2
if nums[middle] > target:
right = middle # The target is in the left interval, within [left, middle).
elif nums[middle] < target:
left = middle + 1 # The target is in the right interval, within [middle + 1, right).
else:
return middle # Find the target value in the array and return the index directly.
return -1 # Did not find the target value- Time complexity: O(log n)
- Space complexity: O(1)
Summary
The binary search is a very important fundamental algorithm. Why do many people find that they can understand it at a glance but fail to implement it?
The main reason is that they do not have a clear understanding of the definition of the interval and fail to consistently handle boundaries according to the definition of the search interval during the loop.
The definition of an interval is an invariant, so adhering to this definition for boundary handling in loops follows the rule of loop invariants.
This article presents two common definitions of intervals and provides two implementations of binary search. Each boundary handling method is explained in detail based on the definitions of intervals.
I believe that after reading this article, you should have a deeper understanding of binary search.

Discussion