226. Invert Binary Tree

LeetCode Link: 226. Invert Binary Tree

Problem Statement

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

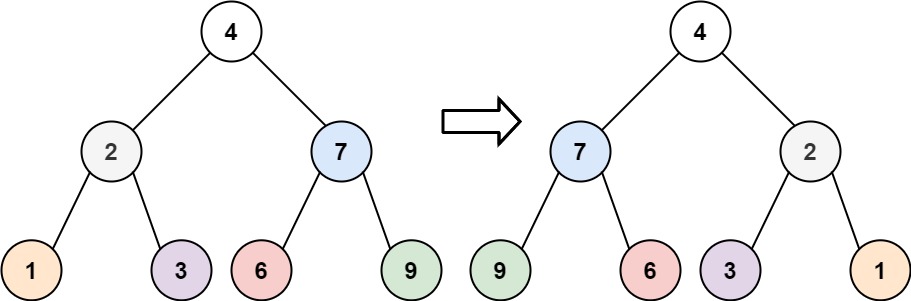
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:

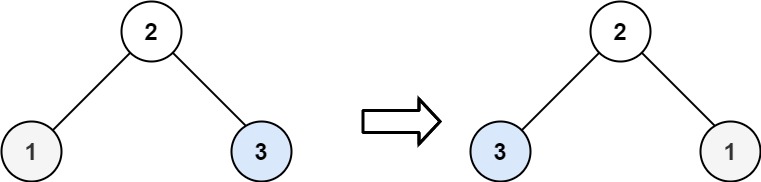
Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Understanding the Problem

At its core, inverting a binary tree involves processing every node and swapping its left and right children. The challenge, however, lies in how you traverse the tree to ensure every node is visited and processed correctly.

Key Points:

Traversal Order:
The order in which you traverse the tree (pre-order, in-order, post-order, or level-order) is crucial. Each approach affects when the swapping operation is performed.
Swapping Logic:
In Python, swapping two variables is elegantly handled by tuple unpacking:

node.left, node.right = node.right, node.left

Recursive vs. Iterative:
The inversion problem can be solved using both recursive methods and iterative methods (using stacks or queues).

Tree Traversals and Their Role

Understanding different tree traversals is essential, in the previous post, I have already talked about different ways to traverse binary trees:

Pre-order Traversal (Root-Left-Right):
- Process: Visit the root first, swap the children, then recursively process the left and right subtrees.
- Insight: Swapping at the root before diving into subtrees ensures that all nodes are processed in a top-down manner.
Post-order Traversal (Left-Right-Root):
- Process: Recursively invert the left subtree, then the right subtree, and finally swap the children of the current node.
- Insight: This approach processes the children first before swapping, which can be beneficial when the swap needs to occur after ensuring both subtrees are already inverted.
In-order Traversal (Left-Root-Right):
- Caveat: A straightforward in-order traversal can lead to nodes being swapped twice, which might undo the inversion. Special handling is required if you choose to use in-order traversal.
Level-order Traversal (Breadth-First Search):
- Process: Use a queue to traverse the tree level by level, swapping the children of each node as you dequeue them.
- Insight: This method is intuitive for those familiar with iterative processing and ensures that nodes are processed in order of their depth in the tree.

Python Implementation Strategies

TreeNode Class Definition

Before diving into the solutions, let's understand the binary tree node structure we'll be working with:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val          # Node's value
        self.left = left        # Left child reference
        self.right = right      # Right child referenc

Below, we outline several Python solutions with detailed explanations for each approach.

Recursive Approach

Pre-order Traversal (Root → Left → Right)

In a recursive pre-order approach, we first swap the children at the current node, then recursively apply the same logic to the children.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        # Base case: if the node is None, just return None
        if not root:
            return None
        
        # Swap the left and right children using tuple unpacking
        root.left, root.right = root.right, root.left
        
        # Recursively invert the left and right subtrees
        self.invertTree(root.left)
        self.invertTree(root.right)
        
        return root

This approach is particularly intuitive because we swap the children first, then recursively process the subtrees. The swapping happens at the parent level before we move to the children.

In-order Traversal (Left → Root → Right)

While in-order traversal can work, it requires careful handling to avoid double-swapping:

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        
        # Process left subtree
        self.invertTree(root.left)
        
        # Process current node
        root.left, root.right = root.right, root.left
        
        # Important: Process the new left subtree (originally right)
        self.invertTree(root.left)
        return root

Notice that after swapping, we process the new left child (which was originally the right child). This is crucial to avoid processing the same subtree twice.

Post-order Traversal (Left → Right → Root)

Another method is to invert the subtrees first and then swap the children at the current node.

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        
        # First, recursively invert the left and right subtrees
        self.invertTree(root.left)
        self.invertTree(root.right)
        
        # After the subtrees have been inverted, swap the children of the current node
        root.left, root.right = root.right, root.left
        
        return root

This approach processes the deepest nodes first, working its way up to the root. It's like building the inverted tree from the bottom up.

Iterative Solutions

Stack-based Pre-order Traversal

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        
        stack = [root]
        while stack:
            # Process current node
            node = stack.pop()
            node.left, node.right = node.right, node.left
            
            # Push children to stack (right first to maintain pre-order)
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return root

The right child is pushed first so that the left child will be processed first (since we're using a stack's LIFO property).

Modified Stack-based Traversal

This version demonstrates a different way to handle node processing:

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        
        stack = [root]
        while stack:
            node = stack.pop()
            
            # Order of pushing children affects traversal pattern
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
                
            # Swap children
            node.left, node.right = node.right, node.left
        return root

While this looks similar to post-order traversal, it's actually still performing pre-order operations with different node processing timing.

Level-order Traversal (Breadth-First Search)

Using a queue for level-by-level processing:

from collections import deque

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        
        queue = deque([root])
        while queue:
            # Process each level
            node = queue.popleft()
            node.left, node.right = node.right, node.left
            
            # Add children to queue for next level
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        return root

This approach processes the tree level by level, which can be particularly useful when you want to visualize the inversion process layer by layer.

Comparing the Approaches

Memory Usage:
- Recursive: O(h) space where h is tree height (due to call stack)
- Stack-based: O(w) space where w is maximum tree width
- Queue-based: O(w) space where w is maximum tree width
Time Complexity:
- All approaches: O(n) where n is number of nodes
- Each node is processed exactly once
Use Cases:
- Recursive: Clearest implementation, good for balanced trees
- Stack-based: Better for deep trees (avoids stack overflow)
- Level-order: Best for level-by-level processing or visualization

Remember that while all these approaches achieve the same result, each has its strengths depending on the specific requirements of your application, such as memory constraints, tree structure, or processing order needs.

Pitfalls and Considerations

Multiple Swaps in In-order Traversal:
A naive in-order traversal may swap a node’s children twice, effectively nullifying the inversion. While there are workarounds, they often result in a traversal that resembles pre-order or post-order.
Choosing the Right Traversal:
Both recursive and iterative methods have their pros and cons. Recursive solutions are typically easier to understand and write but may hit recursion limits for very deep trees. Iterative solutions, using DFS or BFS, are more robust in these scenarios.

Conclusion

The binary tree inversion problem, despite its apparent simplicity, teaches us valuable lessons about tree traversal, recursion, and the importance of choosing the right approach for a given problem. While the solution might be straightforward, understanding the various approaches and their implications helps build a stronger foundation in tree manipulation algorithms.

Remember: sometimes the simplest problems can teach us the most profound lessons in computer science. Whether you're preparing for interviews or working on real-world applications, understanding these fundamentals is crucial for success in software development.