Problem Definition
Given an integer array Array, please calculate the sum of elements in each specified interval.
Input Description
The first line of input is the length n of the integer array Array, followed by n lines, each containing one integer representing an element of the array. The subsequent input consists of intervals for which sums need to be calculated, until the end of the file.
Output Description
Output the sum of elements for each specified interval.
Input Example
5
1
2
3
4
5
0 1
1 3Output Example
3
9Data Range: 0 < n <= 100000
Thought Process
In this question, we will explain a commonly used problem-solving technique for arrays: prefix sums.
The idea behind prefix sums is to reuse the sum of previously calculated subarrays to reduce the number of cumulative calculations needed for interval queries.
Prefix sums are very useful when it comes to calculating range sums!
The concept of prefix sums is actually quite simple, and I'll give you an example that makes it easy to understand.
For instance, if we want to calculate the range sum on the array vec[i].
We first perform cumulative addition, where p[i] represents the sum of vec[i] from index 0 to i.
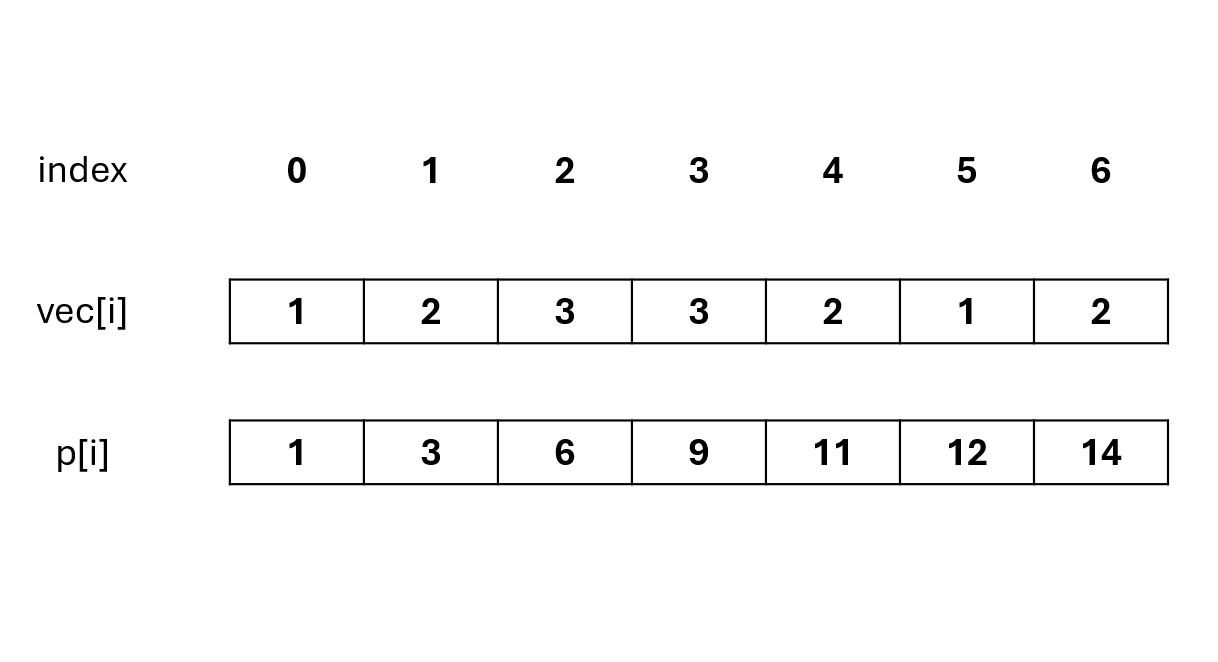
If we want to calculate the cumulative sum between index 2 and index 5 in the vec array, we can just use p[5] - p[1]:
p[1] = vec[0] + vec[1];
p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
Isn't this exactly the cumulative sum we are looking for between index 2 and index 5?
As shown in the figure:
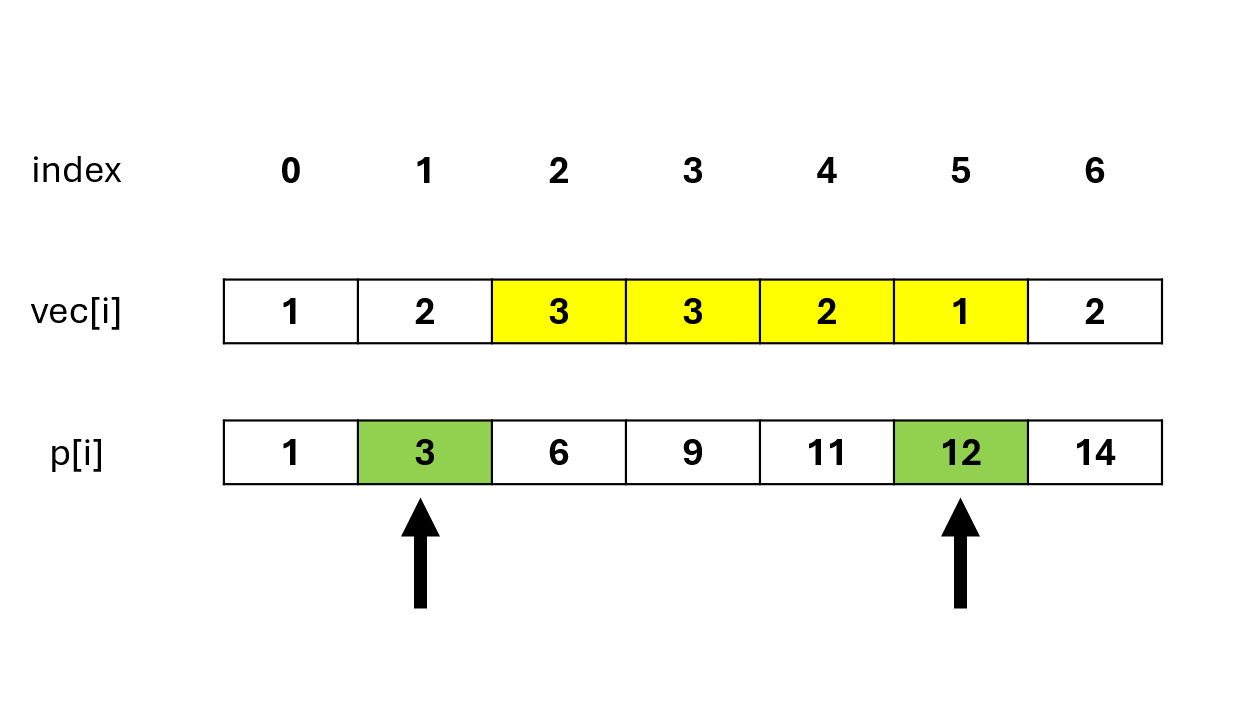
p[5] - p[1] is the sum of the interval in the red part.
The p array is the cumulative sum we calculated earlier, so every time we need to find an interval sum afterwards, we only need O(1) operations.
Note: When using prefix sums for calculations, pay special attention to how you determine intervals.
As shown in the figure above, if we want to calculate the interval sum for indices [2, 5], it should be p[5] - p[1], not p[5] - p[2].
Solution
class RangeSum:
def __init__(self, nums: List[int]):
"""
Initialize prefix sum array from the input array
"""
n = len(nums)
self.prefix = [0] * n
self.prefix[0] = nums[0]
for i in range(1, n):
self.prefix[i] = self.prefix[i-1] + nums[i]
def sumRange(self, left: int, right: int) -> int:
"""
Return sum of numbers between index left and right inclusive
"""
if left == 0:
return self.prefix[right]
return self.prefix[right] - self.prefix[left-1]
Discussion