Hash Table Theoretical Foundations

What is a Hash Table? A hash table is a data structure that lets you access values using unique keys. Like an array, where you use indices to instantly retrieve elements, a hash table uses keys to look up stored data directly.

What Problems Do Hash Tables Solve?

Hash tables provide an efficient solution for determining whether elements exist within a set.

A practical example is verifying student enrollment in a school database. While a traditional enumeration approach would require checking each student sequentially with O(n) time complexity, a hash table reduces this operation to O(1) constant time.

The implementation requires an initial setup where student names are stored in the hash table. Subsequently, verification of enrollment becomes a straightforward indexing operation, facilitated by a hash function that maps student names to specific locations in the table. This approach significantly optimizes the search process and improves system performance.

Hash Function

A hash function serves as the mechanism for converting student names into specific array indices within the hash table. This conversion process occurs through a hashCode operation, which employs a standardized encoding methodology to transform diverse data types into distinct numerical values. Through this process, each student name receives a corresponding numerical index in the hash table, enabling efficient retrieval.

The hashCode function effectively creates a mapping system that translates the abstract concept of a student name into a concrete location within the data structure. This transformation facilitates rapid verification of student enrollment through direct index access.

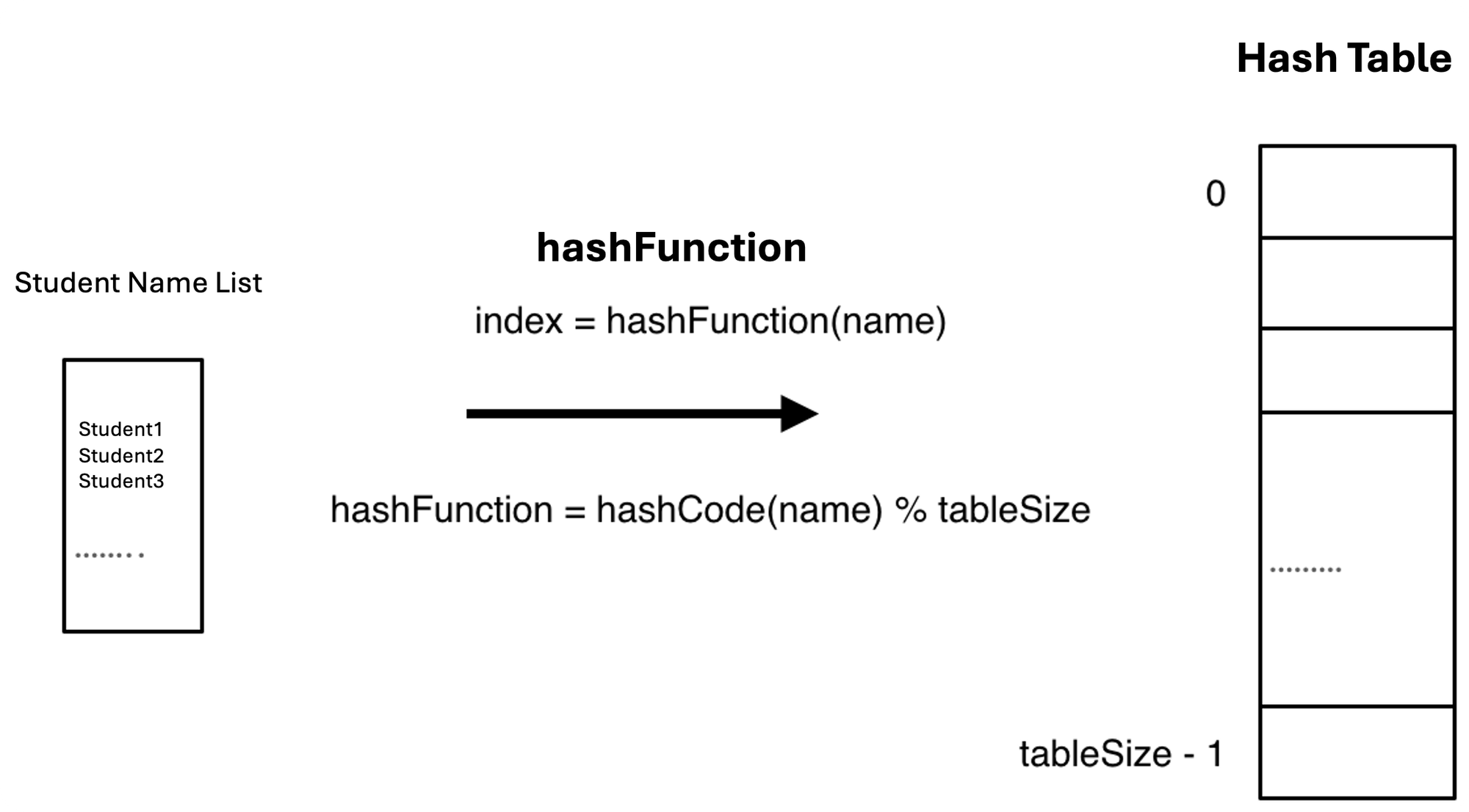
When a hashCode generates a value exceeding the hash table's size (tableSize), we implement a modulo operation to ensure the resulting index falls within valid bounds. This mathematical adjustment guarantees that all student names map to legitimate positions within the hash table.

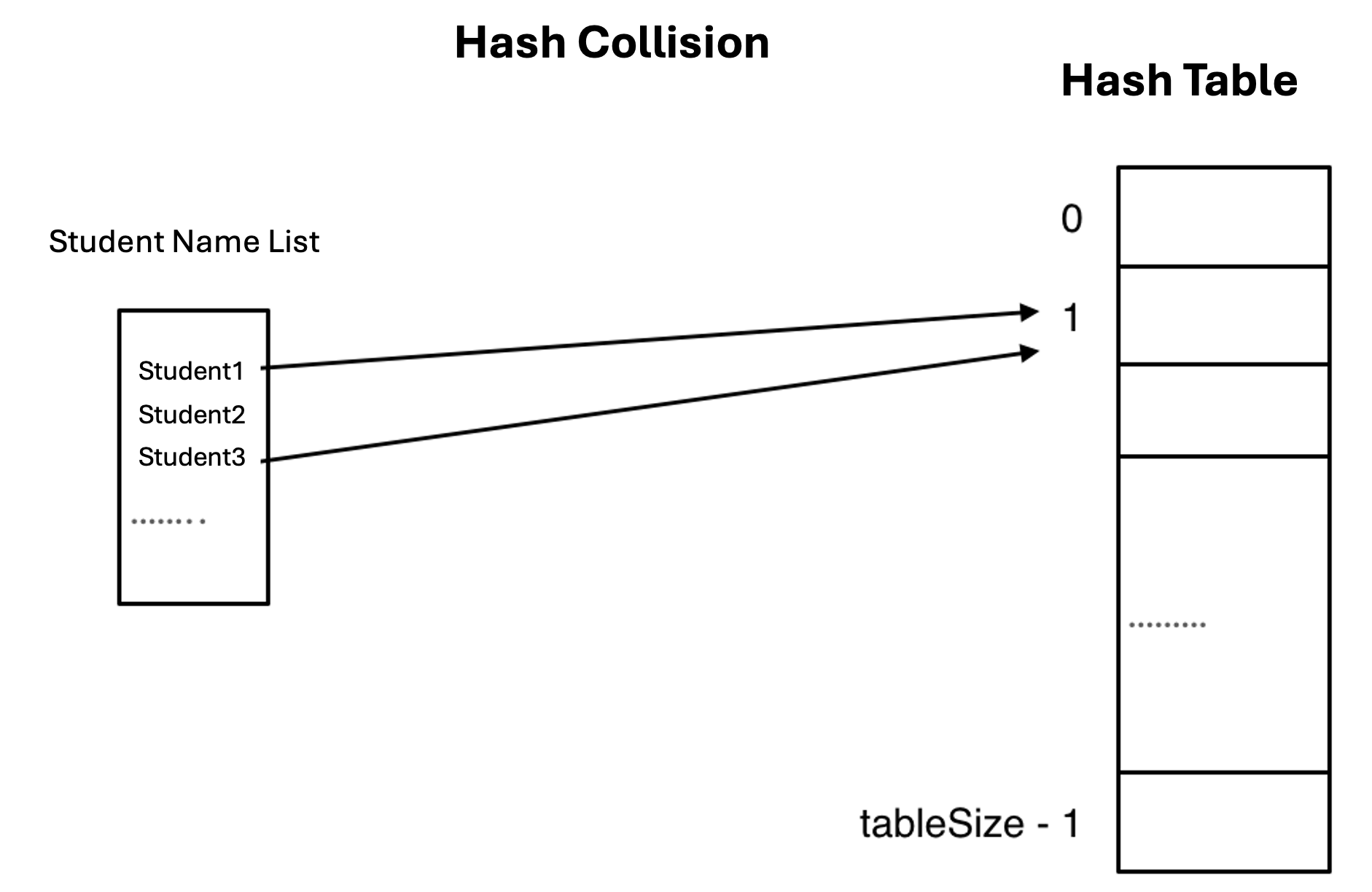
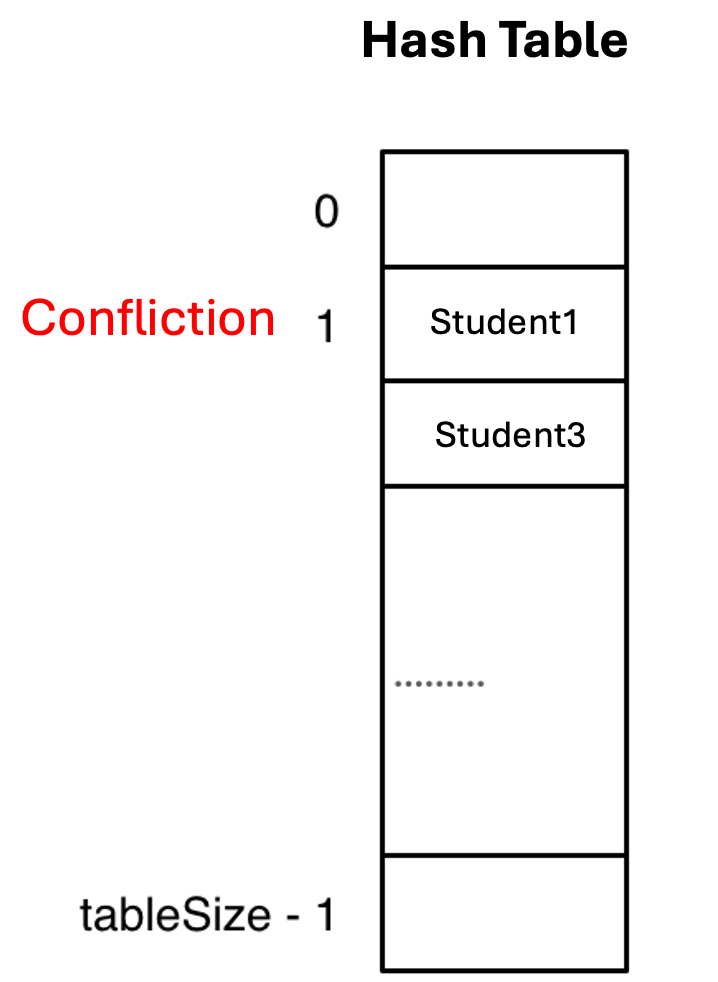
However, this solution introduces a notable challenge: the potential for hash collisions. Given that a hash table functions as an array with finite size, situations arise where the number of students surpasses the table's capacity. Even with an optimally designed hash function that distributes values uniformly, multiple student names may inevitably map to identical index positions.

Hash Collision

When multiple elements map to the same index position in a hash table, we encounter what is known as a hash collision.

In the given example, both Student1 and Student3 have been assigned to index position 1 through the hash function's calculation. This situation exemplifies a fundamental challenge in hash table implementation that requires careful consideration and appropriate resolution strategies.

Two standard approaches address the challenge of hash collisions: chaining and linear probing. Each method provides a systematic solution for managing situations where multiple elements map to the same index position in a hash table.

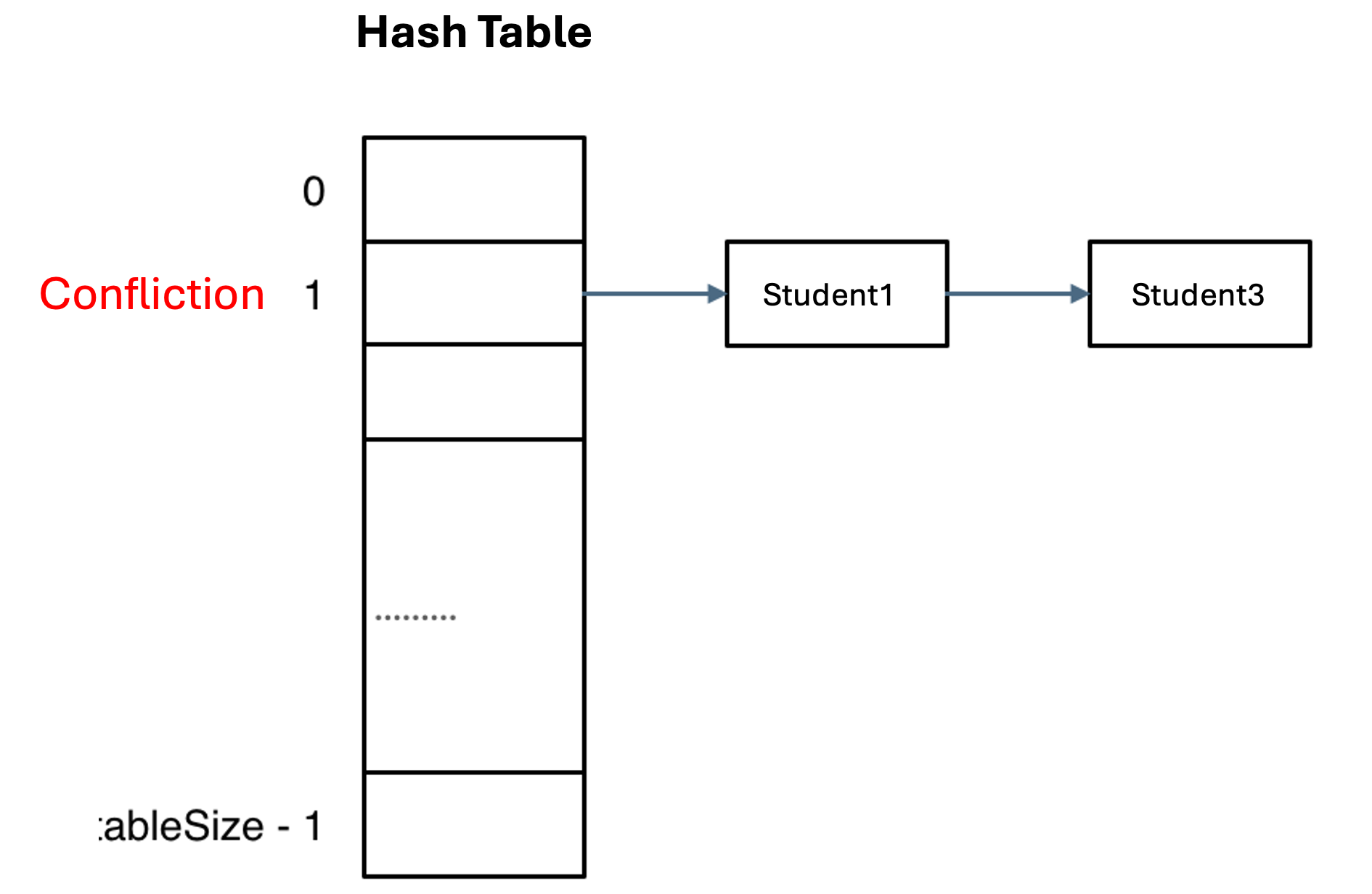
Chaining Method for Collision Resolution

When hash collisions occur, as in the case where Student1 and Student3 map to index position 1, the chaining method provides an elegant solution. This approach implements a linked list at each index position to store multiple elements that share the same hash value. When accessing the data, we first locate the correct index, then traverse the linked list to find the specific element.

This structured approach maintains efficient data organization while accommodating multiple entries at the same index position. The implementation ensures that no data is lost due to collisions, and all elements remain accessible through their respective index positions.

Linear Probing for Collision Resolution

Linear probing offers an alternative approach to handling hash collisions, with a fundamental requirement that the hash table size (tableSize) must exceed the volume of data to be stored (dataSize). This prerequisite ensures sufficient vacant positions within the table to accommodate collision resolution.

In implementation, when Student1 occupies the initially calculated position, the algorithm systematically searches for the next available empty slot to place Student3's information. This sequential search continues until a suitable vacant position is identified. This approach effectively utilizes the hash table's empty capacity to resolve collision scenarios, though it necessitates careful capacity planning to maintain adequate vacant positions for potential collisions.

The success of this method depends on maintaining an appropriate ratio between the table size and the amount of data stored, ensuring efficient resolution of collision scenarios while optimizing space utilization.

Common Hash Structures in Python

When solving problems using hashing techniques in Python, three commonly used data structures come into play:

• Lists
• Sets
• Dictionaries

While lists are straightforward and familiar, let's delve deeper into sets and dictionaries to explore their implementation, characteristics, and usage. These structures provide Python developers with powerful tools for efficient hashing operations.

Set

In Python, sets are collections of unique elements. They come in two flavors:

• set: Mutable and widely used for operations involving unique elements. It supports adding and removing elements with average O(1) complexity.
• frozenset: An immutable version of set. Useful in scenarios where a hashable collection of unique elements is required, such as using it as a key in a dictionary.

The underlying implementation of both is a hash table, which makes operations like lookup, addition, and deletion very efficient on average.

Dictionary (Map)

In Python, dictionaries are key-value pairs, where each key must be unique and hashable. The value, however, has no such restrictions. Python provides two main dictionary-like structures:

• dict: The standard dictionary in Python, implemented using a hash table. Starting with Python 3.7, dictionaries maintain the insertion order of keys. Operations like key lookup, addition, and deletion are O(1) on average.
• defaultdict: A subclass of dict from the collections module. It provides a default value for nonexistent keys, simplifying certain programming patterns.

Key Differences and Use Cases

• Efficiency: For most hash-based operations, set and dict provide O(1) average-case complexity for lookups and modifications.
• Immutability: If immutability is required, use frozenset for sets. For dictionaries, a workaround might involve tuples of key-value pairs or third-party immutable libraries like types.MappingProxyType.
• Ordered Data: Python's dict and set maintain insertion order (starting with Python 3.7), though ordering is not guaranteed for all set operations.

When to Use What

1. Set Operations:
   • Use set when you need fast membership tests, like checking if an element exists.
   • Use frozenset when a hashable, immutable collection of unique elements is required.
2. Mapping Operations:
   • Use dict when you need key-value associations with fast lookup.
   • Use defaultdict when you need a default value for missing keys (e.g., for counting occurrences or grouping).

Conclusion

When faced with problems requiring rapid element lookup within a collection, hash tables emerge as an optimal solution. This fundamental data structure offers a powerful trade-off: exchanging additional memory usage for dramatically improved search performance.

The efficiency gains of hash-based approaches become particularly valuable in scenarios requiring frequent membership testing or data retrieval. By utilizing additional space through arrays, sets, or maps, we achieve the near-instantaneous access that makes hash tables indispensable in modern software development.

For software engineers approaching technical interviews or real-world programming challenges, hash tables should be a primary consideration whenever element verification becomes a key requirement. Their ability to deliver consistent O(1) average-case lookup complexity often provides the optimal balance between implementation complexity and performance.

Understanding this space-time trade-off and recognizing scenarios where hash tables provide the most benefit represents a crucial skill in algorithmic problem-solving. While the memory overhead must be considered, the performance advantages frequently justify this resource allocation, particularly in applications where lookup speed is paramount.