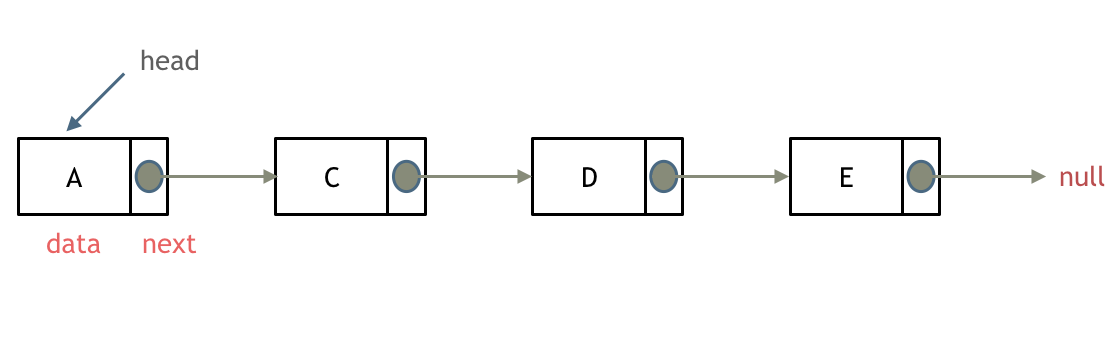
A linked list is a linear data structure in which elements are connected through pointers. Each node in the linked list consists of two parts:
- Data field – stores the actual data.
- Pointer field – stores the address of the next node in the sequence.
The pointer field of the last node points to null (representing the end of the list).
The starting node of a linked list is called the head node, also known as the head.
Types of Linked Lists
Now, let's discuss the different types of linked lists:
1. Singly Linked List
This is the basic form of a linked list that we just mentioned.
- In a singly linked list, each node contains one pointer field that points to the next node in the sequence.
- The last node's pointer field points to
null(indicating the end of the list).
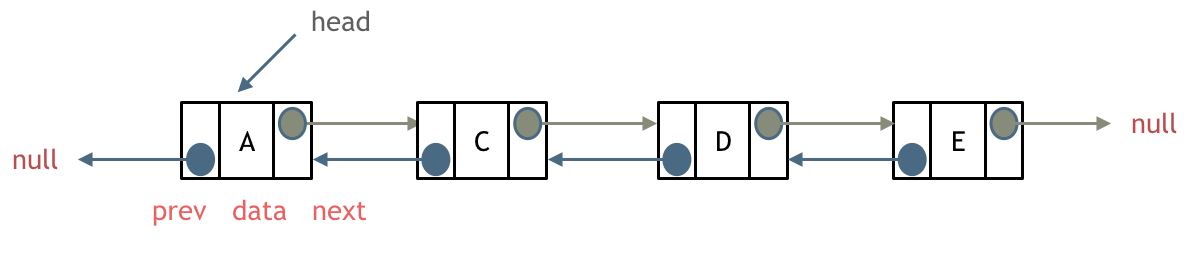
2. Doubly Linked List
In a doubly linked list, each node contains two pointer fields:
- One pointer points to the next node.
- The other pointer points to the previous node.
Since each node has two pointers, the doubly linked list allows bidirectional traversal:
- You can traverse forward through the next pointers.
- You can traverse backward through the previous pointers.
This makes operations like searching, insertion, and deletion more flexible but also slightly more memory-intensive, as each node stores an additional pointer.
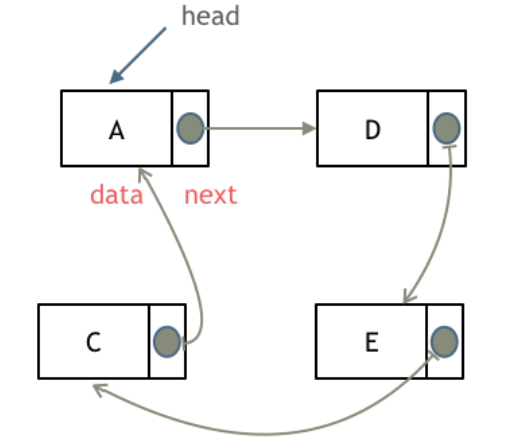
3. Circular Linked List
As the name suggests, a circular linked list connects the last node back to the first node, forming a circle.
- In a singly circular linked list, the last node’s pointer points to the head node.
- In a doubly circular linked list, both the first and last nodes are connected to each other in both directions.
Since there is no null pointer, circular linked lists do not have a natural end, making them ideal for cyclical processes or tasks that require continuous looping.
Application: Solving the Josephus Problem
The Josephus problem is a theoretical puzzle where people are arranged in a circle, and every nth person is eliminated until only one person remains.
A circular linked list is commonly used to model this problem, as it efficiently handles the repeated traversal and elimination in a circular manner.
Storage Method of Linked Lists
After understanding the types of linked lists, let's talk about how linked lists are stored in memory.
Unlike arrays, where elements are stored contiguously in memory, linked lists are stored non-contiguously.
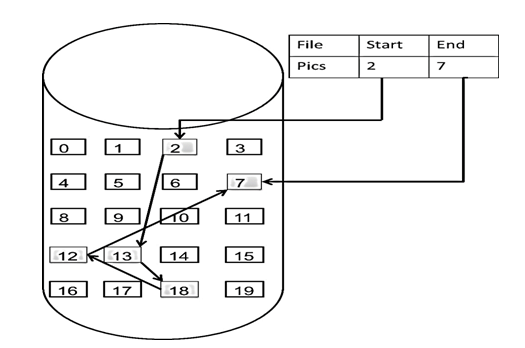
This linked list starts with node 2 and ends with node 7, with each node distributed across different memory address spaces. The nodes are connected together through pointers stored in the pointer fields of each node, forming the complete linked structure.
Key Characteristics of Linked List Storage
- Dynamic Memory Allocation: Each node is allocated memory independently at runtime, based on the system’s memory management.
- Pointers for Connection: The nodes are linked by the pointers stored in the pointer fields of each node.
- Scattered Memory Locations: Since the nodes do not need to be contiguous, they are scattered across random memory addresses, with the pointers forming the connections between them.
Why is Memory Distribution Different from Arrays?
- Arrays: All elements are allocated in a single block of contiguous memory, which can lead to memory waste if the array size is overestimated.
- Linked Lists: Memory is allocated on-demand for each node, making linked lists more efficient for dynamic memory management. However, since nodes are scattered across memory, linked lists rely on the operating system's memory management to allocate appropriate addresses.
This non-contiguous nature of linked lists provides flexibility, allowing for easy insertion and deletion of nodes without the need to shift elements as in arrays.
Definition of a Linked List
Now, let’s talk about the definition of a linked list.
Many people struggle to write the correct definition of a linked list node during interviews. This is often because, when solving problems on platforms like LeetCode, the node definitions are usually predefined, so candidates don’t get much practice defining them from scratch.
However, during interviews, you might be required to write the node structure yourself, and mistakes are common. To help you prepare, here’s an example of how to define a singly linked list node in Python.
class ListNode:
def __init__(self, value=0, next=None):
self.value = value # Data field to store the node's value
self.next = next # Pointer field to store the reference to the next node
# Example usage:
node1 = ListNode(2) # Create a node with value 2
node2 = ListNode(3) # Create a node with value 3
node1.next = node2 # Link node1 to node2Operations on Linked Lists
Deleting a Node
Let’s walk through the process of deleting a node (in this case, Node D) from a linked list.
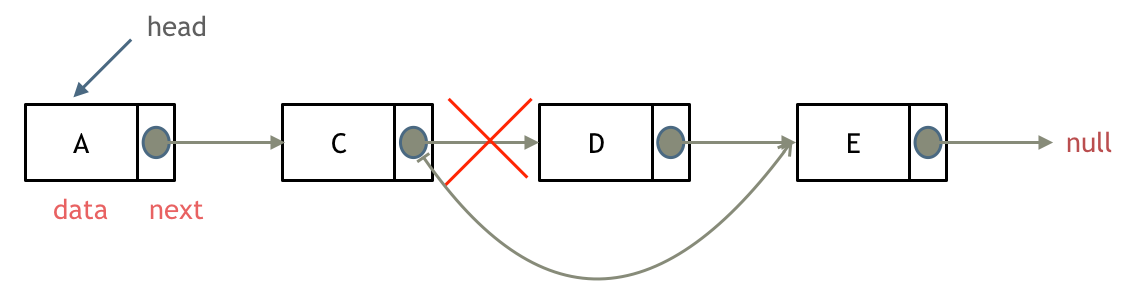
Simply redirect Node C's next pointer to Node E.
Adding a Node
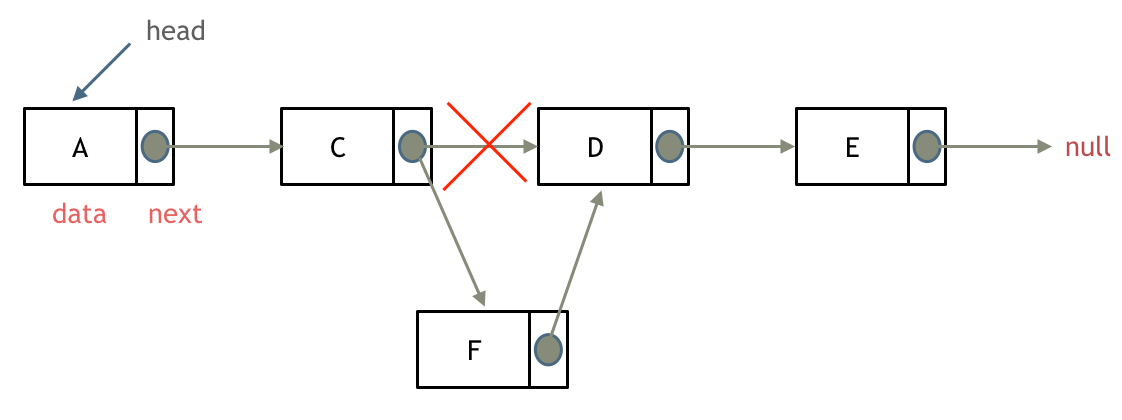
It can be observed that insertion and deletion in a linked list are O(1) operations, as they do not affect other nodes.
However, it’s important to note that if you want to delete the fifth node, you first need to traverse from the head node to the fourth node. Only after locating the fourth node can you use its next pointer to perform the deletion.
The time complexity for this search operation is O(n), as you need to traverse the list to find the target node.
Performance Analysis
Let’s compare the characteristics of linked lists and arrays:
| Feature | Array | Linked List |
|---|---|---|
| Memory Layout | Contiguous memory allocation | Non-contiguous, scattered memory allocation |
| Insertion/Deletion | O(n) – Requires shifting elements | O(1) – Just update pointers |
| Access Time (Query) | O(1) – Direct access via index | O(n) – Must traverse nodes sequentially |
| Memory Efficiency | Wastes memory if allocated more than needed | Efficient, as nodes are created dynamically |
| Fixed Size | Fixed size, defined during allocation | Flexible size, grows or shrinks as needed |
| Usage Scenario | Best for frequent querying and less modification | Best for frequent modification and less querying |
The length of an array is fixed when it is defined. If you want to change the length of the array, you need to redefine a new array.
The length of a linked list can be variable and can be dynamically increased or decreased, making it suitable for scenarios with an unpredictable amount of data, frequent additions and deletions, and fewer queries.

Discussion