102. Binary Tree Level Order Traversal

Mastering level order traversal of binary trees will help you solve the following ten problems in one go:

Problem Statement

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Example 1:

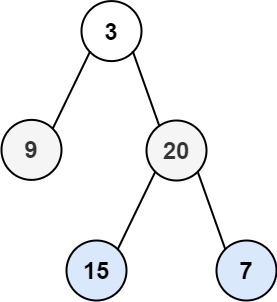
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]

Example 2:

Input: root = [1]
Output: [[1]]

Example 3:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 2000].
-1000 <= Node.val <= 1000

Thought Process

Previously, we have covered three articles on depth-first traversal of binary trees:

Now, let's explore another traversal technique: level order traversal.

Understanding Level Order Traversal

Level order traversal processes nodes level by level, from left to right. Unlike depth-first traversal (preorder, inorder, postorder), level order traversal requires an auxiliary data structure: a queue.

Why use a queue?

A queue follows the First In, First Out (FIFO) principle, which naturally aligns with the order in which nodes should be visited level by level.
In contrast, a stack follows Last In, First Out (LIFO), which is better suited for recursive depth-first traversal.

Implementation

Using a queue, we can implement Breadth-First Search (BFS) on a binary tree.

This ensures that nodes are visited level by level from left to right.

Below is the Python implementation. This template can be used as a foundation to solve all ten problems listed earlier.

Iterative Approach Using a Queue

from collections import deque
from typing import List, Optional

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []
        
        queue = deque([root])
        result = []
        
        while queue:
            level = []
            for _ in range(len(queue)):
                cur = queue.popleft()
                level.append(cur.val)
                if cur.left:
                    queue.append(cur.left)
                if cur.right:
                    queue.append(cur.right)
            
            result.append(level)
        
        return result

Recursive Approach

from typing import List, Optional

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
        if not root:
            return []

        levels = []
        
        def traverse(node, level):
            if not node:
                return
            
            if len(levels) == level:
                levels.append([])
            
            levels[level].append(node.val)
            traverse(node.left, level + 1)
            traverse(node.right, level + 1)
        
        traverse(root, 0)
        return levels

Summary

Level order traversal processes nodes in a left-to-right, level-by-level manner.
A queue (FIFO structure) is essential for implementing level order traversal iteratively.
The recursive approach maintains a list of lists where each sublist represents a level in the tree.
Understanding this traversal method sets the foundation for tackling various tree-based problems efficiently.