Problem Definition

LeetCode Link: 15. 3Sum

Given an integer array nums, return all the triplets [nums[i], nums[j], nums[k]] such that i != j, i != k, and j != k, and nums[i] + nums[j] + nums[k] == 0.

Notice that the solution set must not contain duplicate triplets.

Example 1:

Input: nums = [-1,0,1,2,-1,-4]
Output: [[-1,-1,2],[-1,0,1]]
Explanation:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
The distinct triplets are [-1,0,1] and [-1,-1,2].
Notice that the order of the output and the order of the triplets does not matter.

Example 2:

Input: nums = [0,1,1]
Output: []
Explanation: The only possible triplet does not sum up to 0.

Example 3:

Input: nums = [0,0,0]
Output: [[0,0,0]]
Explanation: The only possible triplet sums up to 0.

Constraints:

  • 3 <= nums.length <= 3000
  • -105 <= nums[i] <= 105

Thought Process

At first glance, the 3Sum problem appears similar to other sum-based problems like 2Sum or 4Sum. However, the requirement to avoid duplicate triplets adds an extra layer of complexity. Here's a breakdown of the approach to tackle this problem effectively:

Brute Force Approach:

  1. Iterate through all possible triplet combinations using three nested loops.
  2. Check if the sum of each triplet equals 0.
  3. Collect unique triplets.

Drawbacks:

  • Time Complexity: O(n^3), which is inefficient for large input sizes.
  • High computational overhead due to the extensive number of iterations.

Optimized Approach Using Sorting and Two Pointers:

  1. Sort the array to simplify the process of avoiding duplicates and to use the two-pointer technique effectively.
  2. Iterate through the array, fixing one element and using two pointers to find the other two elements that sum up to 0.

Advantages:

  • Reduces time complexity to O(n^2).
  • Efficiently handles duplicate elements by skipping over them during iteration.

Hashing-Based Approach:

  1. Utilize a hash map (dictionary) to store elements and their indices.
  2. Iterate through pairs of elements and check if the complement that sums to 0 exists in the hash map.

Considerations:

  1. While hashing can help in reducing time complexity, handling duplicates becomes more intricate.
  2. Additional steps are required to ensure that triplets are unique, which can complicate the implementation.

Given these considerations, the Two-Pointer method emerges as the most effective and commonly used solution for the 3Sum problem in Python due to its balance between simplicity and efficiency.

Solution 1: Two-Pointer Technique

How It Works

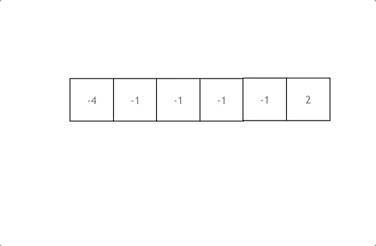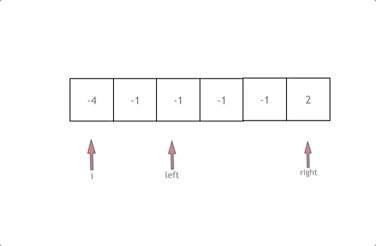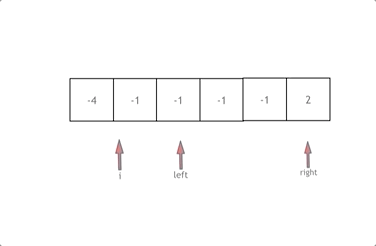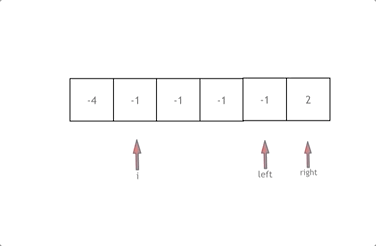
The Two-Pointer technique is an efficient way to solve the 3Sum problem by leveraging a sorted array. Here's the step-by-step reasoning:

  1. Sort the Array:

Sorting helps in easily skipping duplicate elements and allows the use of two pointers moving towards each other to find the desired sum.

  1. Iterate Through the Array:

Fix one element (nums[i]) and use two pointers (left and right) to find the other two elements that sum to 0 with the fixed element.

  1. Adjust Pointers Based on Sum:
  • If the sum of the three elements is less than 0, move the left pointer to the right to increase the sum.
  • If the sum is greater than 0, move the right pointer to the left to decrease the sum.
  • If the sum equals 0, add the triplet to the result and move both pointers, ensuring to skip duplicates.
  1. Avoid Duplicates:

After fixing an element, skip over any duplicate elements to ensure that each triplet is unique.

Similarly, after finding a valid triplet, move the left and right pointers past any duplicates.

Code Explanation

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        result = []
        nums.sort()  # Step 1: Sort the array
        
        for i in range(len(nums)):
            # If the current number is greater than 0, no triplet can sum to 0
            if nums[i] > 0:
                break
            
            # Skip duplicate elements to avoid duplicate triplets
            if i > 0 and nums[i] == nums[i - 1]:
                continue
                
            left, right = i + 1, len(nums) - 1  # Initialize two pointers
            
            while left < right:
                current_sum = nums[i] + nums[left] + nums[right]
                
                if current_sum < 0:
                    left += 1  # Need a larger sum
                elif current_sum > 0:
                    right -= 1  # Need a smaller sum
                else:
                    # Found a triplet that sums to 0
                    result.append([nums[i], nums[left], nums[right]])
                    
                    # Move left and right to the next different numbers to avoid duplicates
                    while left < right and nums[left] == nums[left + 1]:
                        left += 1
                    while left < right and nums[right] == nums[right - 1]:
                        right -= 1
                        
                    left += 1
                    right -= 1
                    
        return result

Step-by-Step Explanation:

  1. Sorting the Array: The nums.sort() function sorts the array in ascending order, which is essential for the two-pointer approach.
  2. Iterating Through the Array:
    • The for loop fixes one element (nums[i]) at a time.
    • If nums[i] is greater than 0, since the array is sorted, no further triplet can sum to 0, so we break out of the loop.
    • If the current element is the same as the previous one, we continue to the next iteration to avoid duplicate triplets.
  3. Initializing Pointers: left is initialized to i + 1, and right is initialized to the last index of the array.
  4. Finding Valid Triplets:
    • Calculate the current_sum of the triplet.
    • If current_sum < 0, move the left pointer to the right to increase the sum.
    • If current_sum > 0, move the right pointer to the left to decrease the sum.
    • If current_sum == 0, append the triplet to result.
  5. Skipping Duplicates:
    • After finding a valid triplet, skip over any duplicate values by moving the left and right pointers past identical elements.
    • This ensures that each triplet in result is unique.

Complexity Analysis

  • Time Complexity: O(n^2)
    • Sorting the array takes O(n log n) time.
    • The main loop runs O(n) times, and the two-pointer search runs O(n) for each iteration, resulting in O(n^2) overall.
  • Space Complexity: O(n) (or O(1) if the sorting is done in place)
    • The space required depends on the sorting algorithm. In Python, the sort() method is typically O(n).

Deduplication Logic

Handling duplicates is a critical aspect of the 3Sum problem, especially when using the Two-Pointer technique. Proper deduplication ensures that the solution set contains only unique triplets without unnecessary computational overhead.

Deduplication of a

When dealing with triplets [a, b, c] corresponding to nums[i], nums[left], and nums[right] respectively, it's essential to handle duplicates for the first element a to prevent redundant triplets.

The Challenge:

  • If the element a is duplicated in the array, naively processing each occurrence can lead to duplicate triplets in the result.

Incorrect approach:

if nums[i] == nums[i + 1]:  # Deduplication operation
    continue
  • Issue: This approach skips the current triplet if the next element is the same as the current one.
  • Consequence: It inadvertently skips valid triplets that contain duplicate elements, such as [-1, -1, 2].

Correct Approach:

if i > 0 and nums[i] == nums[i - 1]:
    continue

Explanation:

  • This condition checks if the current element nums[i] is the same as the previous element nums[i - 1].
  • If it is, the loop continues to the next iteration, effectively skipping the duplicate a element.
  • This ensures that each unique a is processed only once, while still allowing triplets that contain duplicate b and c elements.

Example:

  • Array: [-1, -1, 0, 1, 2]
  • Processing:
    • When i = 0 (first -1), the triplet [-1, 0, 1] is considered.
    • When i = 1 (second -1), the condition nums[i] == nums[i - 1] is True, so this iteration is skipped, avoiding the duplicate triplet [-1, 0, 1] again.

Deduplication of b and c

While deduplicating a is crucial, handling duplicates for b and c is equally important to ensure all triplets in the result are unique.

Common Mistake: Many developers attempt to deduplicate b and c within the main loop, adding additional while loops to skip over duplicates:

while right > left and nums[right] == nums[right + 1]:
    right -= 1
while right > left and nums[left] == nums[left - 1]:
    left += 1

Issue:

  • These additional checks often do not contribute to reducing the overall time complexity.
  • They preemptively skip duplicates without effectively minimizing the number of iterations needed.

Why This Approach Doesn't Improve Efficiency:

  • Redundant Operations: Even without these additional while loops, the existing conditions within the while left < right loop handle moving the pointers appropriately.
  • No Reduction in Iterations: The right-- and left++ operations still decrement or increment the pointers one by one, regardless of these additional checks.
  • No Significant Efficiency Gain: Skipping duplicates in this manner doesn't meaningfully reduce the number of necessary operations since each unique element still needs to be processed.

Solution 2: Dictionary-Based Approach

How It Works

The Dictionary-Based approach leverages Python's dictionary (hash map) to store and count the occurrences of elements. Here's the methodology:

  1. Sort the Array: Sorting is essential to handle duplicates efficiently.
  2. Iterate Through the Array: Fix one element (nums[i]) and use a dictionary to store the counts of elements encountered after the fixed element.
  3. Find Complements:
    • For each subsequent element (nums[j]), calculate the complement that would sum to 0 with nums[i] and nums[j].
    • Check if this complement exists in the dictionary.
    • If it does, add the triplet to the result and update the dictionary to avoid duplicates.
  4. Avoid Duplicates: Similar to the Two-Pointer method, skip over duplicate elements to ensure uniqueness of triplets.

Code Explanation

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
        result = []
        nums.sort()  # Step 1: Sort the array
        
        for i in range(len(nums)):
            # If the current number is greater than 0, no triplet can sum to 0
            if nums[i] > 0:
                break
            
            # Skip duplicate elements to avoid duplicate triplets
            if i > 0 and nums[i] == nums[i - 1]:
                continue
                
            seen = {}
            for j in range(i + 1, len(nums)):
                complement = -nums[i] - nums[j]
                if complement in seen:
                    # Found a triplet
                    triplet = [nums[i], complement, nums[j]]
                    if triplet not in result:
                        result.append(triplet)
                    # Remove the complement to prevent duplicate triplets
                    del seen[complement]
                else:
                    seen[nums[j]] = j  # Store the element and its index
                    
        return result

Avoiding Duplicates:

  • By ensuring that each triplet is only added once and by removing complements after use, the method avoids adding duplicate triplets to result.

Complexity Analysis

  • Time Complexity: O(n^2)
    • Sorting takes O(n log n).
    • The outer loop runs O(n) times.
    • The inner loop also runs O(n) times for each iteration of the outer loop.
    • Thus, the overall time complexity remains O(n^2).
  • Space Complexity: O(n)
    • The dictionary seen can store up to O(n) elements in the worst case.

Note: While the Dictionary-Based approach also achieves O(n^2) time complexity, it may have higher constant factors compared to the Two-Pointer method due to the overhead of dictionary operations. Additionally, handling duplicates requires careful checks, which can introduce complexity into the implementation.

Key Takeaways

  1. Sorting is Fundamental:
    • Sorting the array upfront simplifies the process of avoiding duplicate triplets and enables efficient searching using the Two-Pointer technique.
  2. Two-Pointer Technique is Efficient:
    • For problems involving finding pairs or triplets that satisfy a particular condition, the Two-Pointer method is highly effective, especially when combined with a sorted array.
  3. Handling Duplicates Requires Care:
    • To ensure that the solution set contains only unique triplets, it's crucial to skip over duplicate elements during iteration.
    • Both the Two-Pointer and Dictionary-Based methods incorporate strategies to handle duplicates effectively.
  4. Deduplication Logic Insights:
    • Deduplicating a: Compare the current element with the previous one (nums[i] == nums[i - 1]) to decide whether to skip processing the current triplet.
    • Deduplicating b and c: Avoiding redundant deduplication checks for left and right pointers can simplify the code without affecting performance. The essential deduplication occurs after finding a valid triplet.
  5. Hashing Can Be Useful but Requires Additional Steps:
    • While using a hash map or dictionary can help in finding complements quickly, managing duplicates becomes more involved.
    • The Two-Pointer method often offers a cleaner and more straightforward approach for avoiding duplicates.
  6. Time and Space Trade-offs:
    • Both solutions achieve O(n^2) time complexity, but their space complexities differ.
    • The Two-Pointer method typically uses less additional space compared to the Dictionary-Based approach.
  7. Choosing the Right Approach:
    • Understanding the nature of the problem and the constraints helps in selecting the most suitable algorithm.
    • For 3Sum, the Two-Pointer method is generally preferred due to its efficiency and simplicity in handling duplicates.

Conclusion

The 3Sum problem is an excellent example of how algorithmic strategies like sorting and the Two-Pointer technique can be combined to solve seemingly complex problems efficiently. While the Dictionary-Based approach is also viable, the Two-Pointer method often provides a more elegant and faster solution in practice.

By mastering these techniques, you can tackle a wide range of sum-based problems with confidence and efficiency. Whether you're preparing for technical interviews or enhancing your problem-solving skills, understanding these fundamental approaches is invaluable.