111. Minimum Depth of Binary Tree

LeetCode Link: 111. Minimum Depth of Binary Tree

Problem Statement

Given a binary tree, find its minimum depth.

The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.

Note: A leaf is a node with no children.

Example 1:

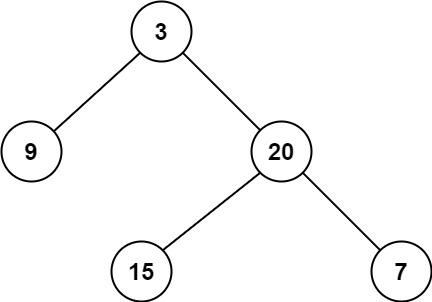
Input: root = [3,9,20,null,null,15,7]
Output: 2

Example 2:

Input: root = [2,null,3,null,4,null,5,null,6]
Output: 5

Constraints:

The number of nodes in the tree is in the range [0, 10⁵].
-1000 <= Node.val <= 1000

Understanding the Problem

After solving the problem of finding the 104. Maximum Depth of Binary Tree , finding the minimum depth might seem straightforward. However, there are some key differences that make this problem a bit trickier.

Both preorder and postorder traversals can be used for this problem. Preorder traversal calculates the depth (from root to a specific node), while postorder traversal calculates the height (from a specific node to leaf).

In the context of binary trees:

Depth of a node: The number of edges or nodes from the root to that particular node
Height of a node: The number of edges or nodes on the longest path from that node to a leaf

When using postorder traversal, we're effectively finding the minimum height of the root node, which is equivalent to the minimum depth of the tree.

A Common Mistake

One of the key challenges with this problem is correctly handling nodes that have only one child. Consider this tree:

Looking at this tree, you might think that the minimum depth is 1 (following the path from node 1), but that's incorrect. The minimum depth is actually 3 (following the path from node 1 to node 4).

This is because the definition of minimum depth specifies it's the distance to the nearest leaf node, and a leaf node must have no children. Node 1 has a child, so it's not a leaf. Node 4 is the first leaf node we encounter, and it's at depth 3.

The key insight is that when calculating minimum depth, we need to find the shortest path to a node that has no children (a leaf node).

Solution Approaches

1. Recursive Approach (Postorder Traversal with Helper Function)

Let's implement the solution following a step-by-step approach:

class Solution:
    def getDepth(self, node):
        if node is None:
            return 0
        leftDepth = self.getDepth(node.left)  # left
        rightDepth = self.getDepth(node.right)  # right
        
        # When left subtree is empty and right is not, this is not the minimum depth path
        if node.left is None and node.right is not None:
            return 1 + rightDepth
        
        # When right subtree is empty and left is not, this is not the minimum depth path
        if node.left is not None and node.right is None:
            return 1 + leftDepth
        
        result = 1 + min(leftDepth, rightDepth)
        return result

    def minDepth(self, root):
        return self.getDepth(root)

2. Recursive Approach (Direct Recursion)

This is a more concise version that integrates the logic directly into the minDepth() function:

class Solution:
    def minDepth(self, root):
        if root is None:
            return 0
        if root.left is None and root.right is not None:
            return 1 + self.minDepth(root.right)
        if root.left is not None and root.right is None:
            return 1 + self.minDepth(root.left)
        return 1 + min(self.minDepth(root.left), self.minDepth(root.right))

3. Recursive Approach (Preorder Traversal)

We can also solve this using preorder traversal by keeping track of the minimum depth found so far:

class Solution:
    def __init__(self):
        self.result = float('inf')

    def getDepth(self, node, depth):
        if node is None:
            return
        if node.left is None and node.right is None:
            self.result = min(self.result, depth)
        if node.left:
            self.getDepth(node.left, depth + 1)
        if node.right:
            self.getDepth(node.right, depth + 1)

    def minDepth(self, root):
        if root is None:
            return 0
        self.getDepth(root, 1)
        return self.result

4. Iterative Approach (Level-Order Traversal)

Level-order traversal (or breadth-first search) is particularly well-suited for this problem because it explores the tree level by level, so the first leaf node encountered will be at the minimum depth:

import collections

class Solution:
    def minDepth(self, root):
        if not root:
            return 0
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1 
            for _ in range(len(queue)):
                node = queue.popleft()
                
                # If we found a leaf node, return the current depth
                if not node.left and not node.right:
                    return depth
            
                if node.left:
                    queue.append(node.left)
                    
                if node.right:
                    queue.append(node.right)

        return depth

Key Differences from Maximum Depth

The primary difference between finding the minimum and maximum depths lies in how we handle nodes with only one child.

For maximum depth, we can simply take the maximum of the left and right subtree depths.
For minimum depth, we need to be careful with nodes that have only one child, as they don't constitute a valid path to a leaf node.

Using our example tree:

If we were calculating maximum depth, we would get 4 (the path 1 → 2 → 3 → 6 or 1 → 2 → 3 → 5). For minimum depth, we get 3 (the path 1 → 2 → 4) because node 4 is the closest leaf node to the root.

Conclusion

The minimum depth problem teaches us the importance of understanding the precise problem definition. The requirement for a leaf node (having no children) creates an interesting twist compared to the maximum depth problem.

When solving tree problems, it's often helpful to visualize the tree and trace through the algorithm to ensure you're handling all edge cases correctly. For this problem specifically, be mindful of how you handle nodes with only one child.

Level-order traversal provides an elegant solution to this problem, as it naturally finds the shortest path to a leaf node. However, the recursive solutions are also instructive for understanding the difference between depth and height in binary trees.